Question

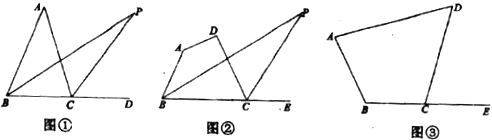
【题目】(1)思考探究：如图①，的内角的平分线与外角的平分线相交于点，请探究与的关系是______.

(2)类比探究：如图②，四边形中，设，，，四边形的内角与外角的平分线相交于点.求的度数.(用，的代数式表示)

(3)拓展迁移：如图③，将(2)中改为，其它条件不变，请在图③中画出，并直接写出_____.(用，的代数式表示)

Answer 1

【答案】(1)；(2)；(3).

【解析】

（1）利用角平分线求出∠PCD=∠ACD,∠PBD=∠ABC,再利用三角形的一个外角定理即可求出.（2）延长BA、CD交于点F，然后根据（1）的结题可得到∠P的表达式.

（3）延长AB、DC交于F,然后根据（1）的结题可得到∠P的表达式.

解：(1)

∵平分，平分，

∴，

∵是的外角

∴

∵是的外角

∴

(2)延长、，交于点.

，

由(1)知：

∴．

（3）延长，交于点. 作与外角的平分线相交于点. 如图：

，