题目内容
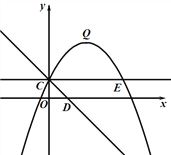
【题目】如图,抛物线![]() 的图象过点C(0,1),顶点为Q(2,3),点D在x轴正半轴上,线段OD=OC.
的图象过点C(0,1),顶点为Q(2,3),点D在x轴正半轴上,线段OD=OC.
(1)求抛物线的解析式;
(2)抛物线上是否存在点M,使得△CDM是以CD为直角边的直角三角形?若存在,请求出M点的坐标;若不存在,请说明理由;
(3)将直线CD绕点C逆时针方向旋转45°所得直线与抛物线相交于另一点E,连接QE.若点P是线段QE上的动点,点F是线段OD上的动点,问:在P点和F点的移动过程中,△PCF的周长是否存在最小值?若存在,求出这个最小值,若不存在,请说明理由.
【答案】(1)![]() ;(2)(2 , 3 )或
;(2)(2 , 3 )或![]() )或
)或![]() ;(3)存在,
;(3)存在, ![]() .
.
【解析】试题分析:
(1)根据已知条件设抛物线解析式为![]() ,代入点C的坐标就可以求出解析式了;
,代入点C的坐标就可以求出解析式了;
(2)①当点C是直角顶点时,由已知求出直线DM的解析式,再把所求解析式和(1)中所求二次函数解析式组合成方程组,解方程组即可求得点M的坐标;②当点D是直角顶点时,同①的方法可求得对应的M的坐标;
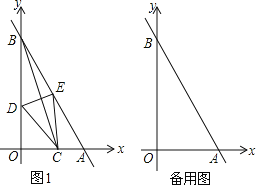
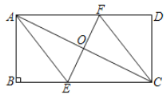
(3)如图3,分别作点C关于直线QE和直线OD的对称点C′和C′′,连接C′C′′交OD于点F,交QE于点P,则△PCF即为符合题意的周长最小的三角形,由轴对称的性质可知,△PCF的周长等于线段C′C″的长度;如图4,连接C′E,作C′N⊥y轴于点N,结合已知条件解出C′C′′的长度即可.
试题解析:
(1)设抛物线的解析式为![]() ,
,
将C(0,1)代入得: ![]() ,
,
解得: ![]() ,
,
∴抛物线的解析式为: ![]() 即
即![]() ;
;
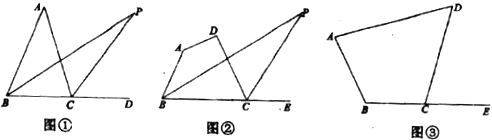
(2)①如图1,当点C为直角顶点时,
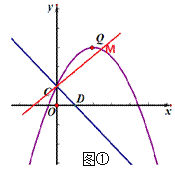
∵点C的坐标为(0,1),
∴OD=OC=1,
∴点D的坐标为(1,0),
设直线CD为![]() ,则:
,则: ![]() ,解答
,解答![]() ,
,
∴直线CD的解析式为: ![]() ,
,
∵此时CM⊥CD,
∴CM的解析式为: ![]() ,
,
由: 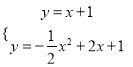 ,解得:
,解得: ![]() ,
, ![]() ,
,
∵点(0,1)与点C重合,
∴点M的坐标为(2,3),此时点M与点Q重合;
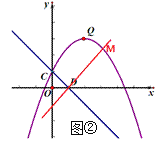
②如图②,当D为直角顶点时,由①可得直线DM的解析式为![]() ,
,
由: 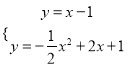 ,解得:
,解得: 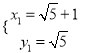 ,
, 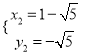 ,
,
∴点M的坐标为为![]() 或
或![]() ;
;
综上所述,符合题意的M有三点,分别是(2 , 3 ), ![]() 或
或![]() .
.
(3) 存在.如图③所示,作点C关于直线QE的对称点C′,作点C关于x轴的对称点C″,连接C′C″,交OD于点F,交QE于点P,则△PCF即为符合题意的周长最小的三角形,由轴对称的性质可知,△PCF的周长等于线段C′C″的长度.
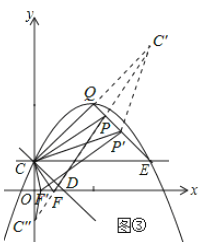
如答图④所示,连接C′E,
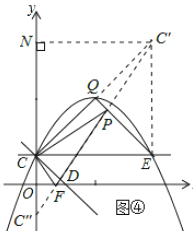
由(2)可知,QC⊥CD, 由题意可得:QC=QE,
∵∠DCE=45°,
∴∠QCE=45°=∠QEC,
∴△QCE是等腰直角三角形,
∵C,C′关于直线QE对称,
∴△QC′E为等腰直角三角形,
∴△CEC′为等腰直角三角形,
∵在抛物线![]() 中,由
中,由![]() 解得
解得![]() ,
,
∴点E的坐标为(4,1),
∴CE=4=C′E,
∴点C′的坐标为(4,5);
∵C,C″关于x轴对称,
∴点C″的坐标为(0,﹣1).
∴OC″=1,
过点C′作C′N⊥y轴于点N,则NC′=CE=4,NC″=4+1+1=6,
在Rt△C′NC″中,由勾股定理得:C′C″=![]() .
.
综上所述,在P点和F点移动过程中,△PCF的周长存在最小值,最小值为![]() .
.