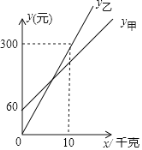
题目内容
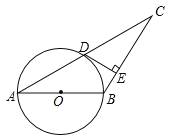
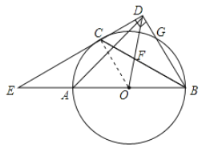
【题目】如图,AB为![]() 的直径,点C和点G是
的直径,点C和点G是![]() 上的两点,过点C作BG的垂线交BG的延长线于点D延长DC交A的延长线于点E,连接BC,交OD于点F,BC平分∠ABD.
上的两点,过点C作BG的垂线交BG的延长线于点D延长DC交A的延长线于点E,连接BC,交OD于点F,BC平分∠ABD.
(1)求证:CD是![]() 的切线;
的切线;
(2)若![]() ,探索线段OF与FD的数量关系;
,探索线段OF与FD的数量关系;
(3)连接AD,若![]() ,
,![]() ,求AD的长.
,求AD的长.

【答案】(1)见解析;(2)![]() ,理由见解析;(3)
,理由见解析;(3)![]()
【解析】
(1)连接OC,然后根据题意和角平分线的性质可以判断OC∥BD,由∠BDC=90°,从而以证明结论成立;
(2)利用![]() 角的性质证得
角的性质证得![]() ,设
,设![]() 的半径为r,证得
的半径为r,证得![]() ,利用同高的两个三角形面积的比等于底的比得到
,利用同高的两个三角形面积的比等于底的比得到![]()
![]() ,继而证得结论;
,继而证得结论;
(3)利用![]() 角的性质求得
角的性质求得![]() ,
,![]() ,利用
,利用![]() 求得
求得![]() ,作
,作![]() ,易求得
,易求得![]() ,
,![]() ,继而求得
,继而求得![]() ,再利用勾股定理即可求得答案.
,再利用勾股定理即可求得答案.
(1)如图,连接OC.
∵![]() ,BC平分
,BC平分![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵OC是![]() 的半径,
的半径,
∴CD是![]() 的切线;
的切线;
(2)![]() .
.
理由如下:
∵![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
设![]() 的半径为r,则
的半径为r,则![]() ,
,![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∵BC平分![]() ,
,
∴F到OB、DB的距离相等,
∴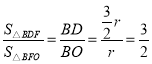 ,
,
∴![]() ,
,
即![]() ;
;
(3)∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
如解图,过点D作![]() 于点M,
于点M,

∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目