Question

【题目】在平面直角坐标系中，横坐标与纵坐标都是整数的点称为整点，如果将二次函数的图象与x轴所围成的封闭图形染成红色，则此红色区域内部及其边界上的整点个数有______ 个

Answer 1

【答案】25

【解析】∵在中，当时，有，

解得：，

∴抛物线与轴的交点坐标为（6.5，0）和（1.5，0），

∵，

∴抛物线的顶点坐标为（4，6.25），

∴抛物线的大致图象如下图所示：

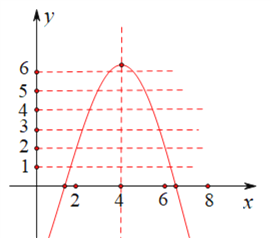
（1）当时，解得：，此时，在直线y=0上，有5个符合要求的整点；

（2）当时，解得：，此时，在直线y=1上，有5个符合要求的整点；

（3）当时，解得：，此时，在直线y=2上，有5个符合要求的整点；

（4）当时，解得：，此时，在直线y=3上，有3个符合要求的整点；

（5）当时，解得：，此时，在直线y=4上，有3个符合要求的整点；

（6）当时，解得：，此时，在直线y=5上，有3个符合要求的整点；

（7）当时，解得：，此时，在直线y=6上有1个符合要求的整点；

综上所述，共有25个整点在所围区域内或其边界上.