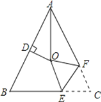
题目内容
【题目】在![]() 中,
中,![]() ,
,![]() 是直线
是直线![]() 上一点,以
上一点,以![]() 为一边在
为一边在![]() 的右侧作
的右侧作![]() ,使
,使![]() ,
,![]() ,连接
,连接![]() .设
.设![]() ,
,![]() .
.

(1)如图(1),点![]() 在线段
在线段![]() 上移动时,试说明
上移动时,试说明![]() ;
;
(2)如图(2),点![]() 在线段
在线段![]() 的延长线上移动时,探索角
的延长线上移动时,探索角![]() 与
与![]() 之间的数量关系并证明;
之间的数量关系并证明;
(3)当点![]() 在线段
在线段![]() 的反向延长线上移动时,请在备用图上根据题意画出图形,并猜想角
的反向延长线上移动时,请在备用图上根据题意画出图形,并猜想角![]() 与
与![]() 之间的数量关系是______________,线段
之间的数量关系是______________,线段![]() 、
、![]() 、
、![]() 之间的数量关系是________________.
之间的数量关系是________________.
【答案】(1)证明见解析;(2)![]() ,理由见解析;(3)
,理由见解析;(3)![]() .
.
【解析】
(1)证明∠CAE=∠BAD,利用SAS定理证明△ABD≌△ACE;
(2)根据△ABD≌△ACE得到∠ABD=∠ACE,根据三角形内角和定理得到角α与β之间的数量关系;
(3)证明△ABD≌△ACE,根据全等三角形的性质得到∠ADB=∠AEC,BD=CE,结合图形解答即可.
解:(1)∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,
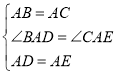 ,
,
∴![]() ,
,
(2)![]() ;理由如下:
;理由如下:
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,
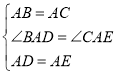 ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,即
,即![]() ;
;
(3)图形如下:
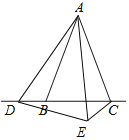
![]() ;
;
如备用图所示:
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,
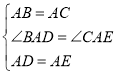 ,
,
∴![]() ,
,
∴![]() ,
,
由三角形内角和定理得:
![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() .
.
故答案为:α=β;BC+CE=DC.

练习册系列答案
相关题目