题目内容
已知关于x的方程(m2-3m+2)x2+(1-2m)x-m(m+1)=0的根是整数,其中m是实数,则m可取的值有( )
| A、3个 | B、4个 | C、5个 | D、6个 |
考点:一元二次方程的整数根与有理根
专题:
分析:分类讨论:①当二次项系数m2-3m+2≠0时,通过对等式左边进行因式分解,即利用因式分解法求得该方程的解,根据限制性条件“关于x的方程(m2-3m+2)x2+(1-2m)x-m(m+1)=0的根是整数”来求m的值;
②当二次项系数m2-3m+2=0时,通过该方程求得m的值,将其代入原方程并求得相应的x值,如果x的值是整数的m值就是符合题意的.
②当二次项系数m2-3m+2=0时,通过该方程求得m的值,将其代入原方程并求得相应的x值,如果x的值是整数的m值就是符合题意的.
解答:解:①当m2-3m+2≠0时,即m≠1和m≠2时,
由原方程,得
[(m-1)x+m][(m-2)x-(m+1)]=0
解得,x=-1-
或 x=1+
,
∵关于x的方程(m2-3m+2)x2+(1-2m)x-m(m+1)=0的根是整数,
∴m=0.5,m=1.5,m=1.25;
②当m2-3m+2=0时,
m=1,m=2,
分别可得x=0,x=2,
因此m=1,m=2也可以;
综上所述,满足条件的m值共有5个.
故选:B.
由原方程,得
[(m-1)x+m][(m-2)x-(m+1)]=0
解得,x=-1-
| 1 |
| m-1 |
| 3 |
| m-2 |
∵关于x的方程(m2-3m+2)x2+(1-2m)x-m(m+1)=0的根是整数,
∴m=0.5,m=1.5,m=1.25;
②当m2-3m+2=0时,
m=1,m=2,
分别可得x=0,x=2,
因此m=1,m=2也可以;
综上所述,满足条件的m值共有5个.
故选:B.
点评:本题考查了一元二次方程的整数根与有理根.解得此题时采用了“分类讨论”的数学思想,以防漏解.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
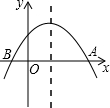 如图,已知抛物线y=x2+bx+c与坐标轴交于A、B两点,则一元二次方程x2+bx+c=0的根的情况是( )
如图,已知抛物线y=x2+bx+c与坐标轴交于A、B两点,则一元二次方程x2+bx+c=0的根的情况是( )| A、没有实数根 |
| B、有两个相等的实数根 |
| C、有两个不相等的实数根 |
| D、可能有实数根,也可能没有实数根 |
将直线y=-2x沿着y轴向下平移3个单位得到直线l,则直线l的解析式是( )
| A、y=-2x+3 |
| B、y=2x-3 |
| C、y=2x+3 |
| D、y=-2x-3 |
 如图,已知AB=DC,∠1=∠2.求证:AC=BD.
如图,已知AB=DC,∠1=∠2.求证:AC=BD.