题目内容
18. 如图所示,一个半径为1的圆内切于一个圆心角为60°的扇形,则扇形的弧长是π.
如图所示,一个半径为1的圆内切于一个圆心角为60°的扇形,则扇形的弧长是π.
分析 连接OA、CB,则CB⊥OB,由切线长定理得出∠BOC=$\frac{1}{2}$×60°=30°,由含30°角的直角三角形的性质得出OC=2CB=2,求出OA=OC+CA=3,扇形的弧长公式即可得出结果.
解答 解:如图所示:连接CB,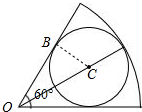
则CB⊥OB,
∴∠OBC=90°,∠BOC=$\frac{1}{2}$×60°=30°,
∵CA=CB=1,
∴OC=2CB=2,
∴OA=OC+CA=3,
∴扇形的弧长=$\frac{60×π×3}{180}$=π.
故答案为:π.
点评 本题考查了相切两圆的性质、切线长定理、含30°角的直角三角形的性质、弧长公式;熟练掌握相切两圆的性质,求出扇形的半径是解决问题的关键.

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
8.若关于x的一元二次方程x2-(b-2)x+b-3=0有两个相等的实数根,则b的值为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
9.方程x(x+2)=0的解是( )
| A. | -2 | B. | 0,-2 | C. | 0,2 | D. | 无实数根 |
13.下列事件中是必然事件的是( )
| A. | 实心铁球投入水中会沉入水底 | B. | 某投篮高手投篮一次就投中 | ||
| C. | 打开电视机,正在播放足球比赛 | D. | 抛掷一枚硬币,落地后正面朝上 |