题目内容
如图,已知∠AOB=α,在射线OA、OB上分别取点OA1=OB1,连结A1B1,在B1A1、B1B上分别取点A2、B2,使B1B2=B1A2,连结A2B2…按此规律上去,记∠A2B1B2=θ1,∠A3B2B3=θ2,…,∠An+1BnBn+1=θn,则θ2013-θ2012的值为( )


分析:根据等腰三角形两底角相等用α表示出∠A1B1O,再根据平角等于180°列式用α表示出θ1,再用θ1表示出θ2,并求出θ2-θ1,依此类推求出θ3-θ2,…,θ2013-θ2012,即可得解.
解答:解:∵OA1=OB1,∠AOB=α,
∴∠A1B1O=
(180°-α),
∴
(180°-α)+θ1=180,
整理得,θ1=
,
∵B1B2=B1A2,∠A2B1B2=θ1,
∴∠A2B2B1=
(180°-θ1),
∴
(180°-θ1)+θ2=180°,
整理得,θ2=
=
,
∴θ2-θ1=
-
=
=
,
同理可求θ3=
=
,
∴θ3-θ2=
-
=
=
,
…,
依此类推,θ2013-θ2012=
.
故选C.
∴∠A1B1O=
| 1 |
| 2 |
∴
| 1 |
| 2 |
整理得,θ1=
| 180°+α |
| 2 |
∵B1B2=B1A2,∠A2B1B2=θ1,
∴∠A2B2B1=
| 1 |
| 2 |
∴
| 1 |
| 2 |
整理得,θ2=
| 180°+θ1 |
| 2 |
| 3×180°+α |
| 4 |
∴θ2-θ1=
| 3×180°+α |
| 4 |
| 180°+α |
| 2 |
| 180°-α |
| 4 |
| 180°-α |
| 22 |
同理可求θ3=
| 180°+θ2 |
| 2 |
| 7×180°+α |
| 8 |
∴θ3-θ2=
| 7×180°+α |
| 8 |
| 3×180°+α |
| 4 |
| 180°-α |
| 8 |
| 180°-α |
| 23 |
…,
依此类推,θ2013-θ2012=
| 180°-α |
| 22013 |
故选C.
点评:本题考查了等腰三角形两底角相等的性质,图形的变化规律,依次求出相邻的两个角的差,得到分母成2的指数次幂变化,分子不变的规律是解题的关键.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
如图,已知∠AOB是直角,∠AOC是锐角,ON平分∠AOC,OM平分∠BOC,则∠MON是( )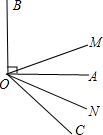

| A、45° | ||
B、45°+
| ||
C、60°-
| ||
| D、不能计算 |


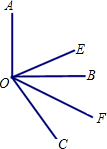 如图,已知∠AOB是直角,∠BOC=60°,OE平分∠AOC,OF平分∠BOC.
如图,已知∠AOB是直角,∠BOC=60°,OE平分∠AOC,OF平分∠BOC. 尺规作图:
尺规作图: 如图,已知∠AOB=x(0°<x<180°),OC平分∠AOB,点N为OB上一个定点.通过画图可以知道:当∠AOB=45°时,在射线OC上存在点P,使△ONP成为等腰三角形,且符合条件的点有三个,即P1(顶点为P2),P2(顶点为0),P3(顶点为N).
如图,已知∠AOB=x(0°<x<180°),OC平分∠AOB,点N为OB上一个定点.通过画图可以知道:当∠AOB=45°时,在射线OC上存在点P,使△ONP成为等腰三角形,且符合条件的点有三个,即P1(顶点为P2),P2(顶点为0),P3(顶点为N).