题目内容
2.若关于x的一元二次方程2x2-2x-3m-1=0有两个实数根x1,x2,且x1x2>x1+x2-4.试求m的取值范围.分析 首先根据根与系数的关系求出x1+x2=1,x1•x2=$\frac{-3m-1}{2}$,然后代入得到关于m的不等式,求出m的取值范围即可.
解答 解:∵关于x的一元二次方程2x2-2x-3m-1=0有两个实数根x1,x2,
∴x1+x2=1,x1•x2=$\frac{-3m-1}{2}$,
∵x1x2>x1+x2-4,
∴$\frac{-3m-1}{2}$>-3,
解得m<$\frac{5}{3}$.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系:若方程两个根为x1,x2,则x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.

练习册系列答案
相关题目
14.下列各数中,是无理数的是( )
| A. | $\sqrt{4}$ | B. | $\frac{22}{7}$ | C. | $\root{3}{8}$ | D. | π-1 |
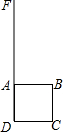 如图,在小路DF的右侧是一片草地,紧靠小路建有一正方形小屋ABCD,现用一根长为6m的牛绳一端系住牛鼻,另一端系在A处.如果小屋的边长为3m,那么这头牛最多能吃掉多大面积的草地?请画出示意图.如果绳长为7m呢?
如图,在小路DF的右侧是一片草地,紧靠小路建有一正方形小屋ABCD,现用一根长为6m的牛绳一端系住牛鼻,另一端系在A处.如果小屋的边长为3m,那么这头牛最多能吃掉多大面积的草地?请画出示意图.如果绳长为7m呢? 已知在⊙O中,P是弧$\widehat{AB}$的中点,C、D是PA、PB的中点,过C、D的直线交圆于E、F,求证:EC=FD.
已知在⊙O中,P是弧$\widehat{AB}$的中点,C、D是PA、PB的中点,过C、D的直线交圆于E、F,求证:EC=FD.