题目内容
南靖云水谣古村落中有一棵高大的老榕树.小明为测量该榕树的高度AD,在大树前的平地上点C处测得大树顶端A的仰角∠C=31°,然后向前直走23米到达B处,又测得大树顶端A的仰角∠ABD=45°,已知C、B、D在同一直线上(如图2),求老榕树的高度AD.(参考数据:tan31°≈
,sin31°≈
)

| 3 |
| 5 |
| 13 |
| 25 |

考点:解直角三角形的应用-仰角俯角问题
专题:
分析:首先分析图形:本题涉及到两个直角三角形△ADB、△ADC,应利用其公共边AD构造等量关系,借助23=
AD-AD构造方程关系式,进而可求出答案.
| 5 |
| 3 |
解答:解:在Rt△ABD中,
∵∠ADB=90°,∠ABD=45°,
∴∠BAD=45°,
∴DB=DA,
在Rt△ACD中,tan31°=
,
∴CD=
=
AD,
∴BC=CD-BD,
∴23=
AD-AD,
∴AD=34.5米,
答:老榕树的高度AD为34.5米.
∵∠ADB=90°,∠ABD=45°,
∴∠BAD=45°,
∴DB=DA,
在Rt△ACD中,tan31°=
| AD |
| CD |
∴CD=
| AD |
| tan31° |
| 5 |
| 3 |
∴BC=CD-BD,
∴23=
| 5 |
| 3 |
∴AD=34.5米,
答:老榕树的高度AD为34.5米.
点评:本题考查俯角、仰角的定义,要求学生能借助俯角、仰角构造直角三角形,并结合图形利用三角函数解直角三角形

练习册系列答案
相关题目


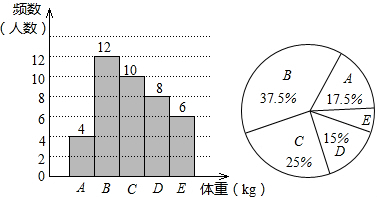 进行抽样调查.已知抽取的样本中,男生、女生的人数相同,利用所得数据绘制如下统计图表:
进行抽样调查.已知抽取的样本中,男生、女生的人数相同,利用所得数据绘制如下统计图表: