题目内容
5.解决问题.学校要购买A,B两种型号的足球,按体育器材门市足球销售价格(单价)计算:若买2个A型足球和3个B型足球,则要花费370元,若买3个A型足球和1个B型足球,则要花费240元.
(1)求A,B两种型号足球的销售价格各是多少元/个?
(2)学校拟向该体育器材门市购买A,B两种型号的足球共20个,且费用不低于1300元,不超过1500元,则有哪几种购球方案?
分析 (1)设A,B两种型号足球的销售价格各是a元/个,b元/个,由若买2个A型足球和3个B型足球,则要花费370元,若买3个A型足球和1个B型足球,则要花费240元列出方程组解答即可;
(2)设购买A型号足球x个,则B型号足球(20-x)个,根据费用不低于1300元,不超过1500元,列出不等式组解答即可.
解答 解:(1)设A,B两种型号足球的销售价格各是a元/个,b元/个,由题意得
$\left\{\begin{array}{l}{2a+3b=370}\\{3a+b=240}\end{array}\right.$
解得$\left\{\begin{array}{l}{a=50}\\{b=90}\end{array}\right.$
答:A,B两种型号足球的销售价格各是50元/个,90元/个.
(2)设购买A型号足球x个,则B型号足球(20-x)个,由题意得
$\left\{\begin{array}{l}{50x+90(20-x)≥1300}\\{50x+90(20-x)≤1500}\end{array}\right.$,
解得7.5≤x≤12.5
∵x是整数,
∴x=8、9、10、11、12,
有5种购球方案:
购买A型号足球8个,B型号足球12个;
购买A型号足球9个,B型号足球11个;
购买A型号足球10个,B型号足球10个;
购买A型号足球11个,B型号足球9个;
购买A型号足球12个,B型号足球8个.
点评 此题考查二元一次方程组与一元一次不等式组的实际运用,找出题目蕴含的等量关系与不等关系是解决问题的关键.

练习册系列答案
相关题目
15.一次函数y=3x+6的图象经过( )
| A. | 第1、2、3象限 | B. | 第2、3、4象限 | C. | 第1、2、4象限 | D. | 第1、3、4象限 |
16.已知一三角形的三条中位线长分别为6、8、10,则这个三角形的周长是( )
| A. | 46 | B. | 48 | C. | 52 | D. | 130 |
13.若a>b,且c<0,则下列不等式中正确的是( )
| A. | a÷c<b÷c | B. | a×c>b×c | C. | a+c<b+c | D. | a-c<b-c |
10.为促进学校之间的友谊,某县教育局组织了中学生友谊篮球赛,要求每两队之间都进行两次比赛,共要比赛90场,问共有多少个学校组队参加比赛?若设共有x个学校组队参加比赛,可列方程为( )
| A. | $\frac{1}{2}x(x-1)=90$ | B. | $\frac{1}{2}x(x+1)=90$ | C. | x(x-1)=90 | D. | x(x+1)=90 |
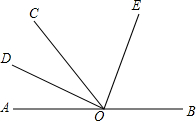 如图,点O为直线AB上一点,∠AOC=50°,OD平分∠AOC.
如图,点O为直线AB上一点,∠AOC=50°,OD平分∠AOC.