题目内容
已知：△ABC中，AD⊥AC，∠BAD=∠C，BD=2，CD=6．（1）求线段AB的长；
（2）求tan∠ACD的值．
考点：相似三角形的判定与性质,解直角三角形
专题：
分析：（1）利用相似三角形的判定方法：有两对角相等的三角形相似可证明△BAD∽△BCA，利用相似三角形的性质：对应边的比值相等即可求出线段AB的长；
（2）因为tan∠ACD=
，（1）可知△BAD∽△BCA，所以
=
，利用已知数据即可求出tan∠ACD的值．
（2）因为tan∠ACD=
| AD |
| AC |
| AD |
| AC |
| AB |
| BC |
解答：解：（1）∵∠BAD=∠C，∠B=∠B，
∴△BAD∽△BCA，
∴
=
，
∵BD=2，CD=6．
∴
=
，
∴AB=4；
（2）∵AD⊥AC，
∴∠DAC=90°，
∴△DAC是直角三角形，
∴tan∠ACD=
，
∵△BAD∽△BCA，
∴
=
，
∴tan∠ACD=
=
=
．
∴△BAD∽△BCA，
∴
| AB |
| CB |
| BD |
| BA |
∵BD=2，CD=6．
∴
| AB |
| 8 |
| 2 |
| AB |
∴AB=4；
（2）∵AD⊥AC，
∴∠DAC=90°，
∴△DAC是直角三角形，
∴tan∠ACD=
| AD |
| AC |
∵△BAD∽△BCA，
∴
| AD |
| AC |
| AB |
| BC |
∴tan∠ACD=
| AD |
| AC |
| 4 |
| 8 |
| 1 |
| 2 |
点评：本题考查了相似三角形的判定和性质以及锐角三角函数中的正切的基本概念，题目比较简单，属于基础性题．
练习册系列答案
相关题目
如图，⊙O内切△ABC于D、E、F，∠B=50°，∠C=60°，则∠FDE的度数为（ ）| A、50° | B、55° |
| C、60° | D、70° |
如图，在⊙O中，AB为直径，AD为弦，过D点的直线与AB的延长线交于点C．已知m、n是方程x2+5x+3=0的两根，则m
+n
的值为（ ）
|
|
A、2
| ||
B、-2
| ||
C、±2
| ||
| D、以上都不对 |
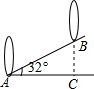如图，坡角为32°的斜坡上两树间的水平距离AC为2米，则两树间的坡面距离AB为（ ）米．| A、2cos32° | ||
| B、2tan32° | ||
| C、2sin32° | ||
D、
|
如图所示，一朵三叶花由六段近似圆弧组成，每一段圆弧都是四分之一圆周，每个叶片两端间的弦长为2，则此三叶花的面积约为