题目内容
10.一个不透明的布袋里装有4个乒乓球,每个求上面分别标有1、2、3、4,从布袋中随机摸取一个乒乓球,记下数字(1)若将第一次摸取的乒乓球放回后,摇匀,再随机摸取第二个乒乓球,记下数字
①请你用树状图或列表法列出所有可能的结果;
②求“两次记下的数字之和大于4且小于7”的概率;
(2)若将第一次摸取的乒乓球记下数字后不放回,再随机摸取第二个乒乓球并记下数字,请直接写出“两次记下的数字之和大于4且小于7”的概率.
分析 (1)根据概率的求法,找准两点:①全部情况的总数;②符合条件的情况数目;二者的比值就是其发生的概率.使用列表法分析时,一定要做到不重不漏.
(2)依据题意先用列表法或画树状图法分析所有等可能和达到某种效果的可能,然后根据概率公式求出该事件的概率.
解答 解:(1)①列表如下,
| 1 | 2 | 3 | 4 | |
| 1 | 1,1 | 1,2 | 1,3 | 1,4 |
| 2 | 2,1 | 2,2 | 2,3 | 2,4 |
| 3 | 3,1 | 3,2 | 3,3 | 3,4 |
| 4 | 4,1 | 4,2 | 4,3 | 4,4 |
∴P(两次记下的数字之和大于4且小于7)=$\frac{7}{16}$;
(2)根据题意画树形图如下:

由以上可知共有12种可能结果分别为:(1,2),(1,3),(1,4),(2,1),(2,3),(2,4),(3,1),(3,2),(3,4),(4,1),(4,2),(4,3);“两次记下的数字之和大于4且小于7”的有(1,4),(2,3),(2,4),(3,2),(4,1),(4,2)6种,
故P(两次记下的数字之和大于4且小于7)=$\frac{6}{12}$=$\frac{1}{2}$;.
点评 此题考查的是用列表法或树状图法求概率.列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
1. 一次函数y=kx+b的图象如图所示,不等式kx+b>0的解集是( )
一次函数y=kx+b的图象如图所示,不等式kx+b>0的解集是( )
 一次函数y=kx+b的图象如图所示,不等式kx+b>0的解集是( )
一次函数y=kx+b的图象如图所示,不等式kx+b>0的解集是( )| A. | x>2 | B. | x>4 | C. | x<2 | D. | x<4 |
18. 某校为了调查学生书写汉字的能力,从八年级800名学生中随机抽选了50名学生参加测试,这50名学生同时听写50个常用汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出不完整的频数分布表和频数分布直方图如图表:
某校为了调查学生书写汉字的能力,从八年级800名学生中随机抽选了50名学生参加测试,这50名学生同时听写50个常用汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出不完整的频数分布表和频数分布直方图如图表:
频数分布表
请结合图表完成下列各题:
(1)求表中a的值;
(2)请把频数分布直方图补充完整;
(3)若测试成绩不低于40分为优秀,请你估计该校八年级汉字书写优秀的人数?
(4)第一组中的A、B、C、D 四名同学为提高汉字书写能力,分成两组,每组两人进行对抗练习,请用列表法或画树状图的方法,求A与B名同学能分在同一组的概率.
 某校为了调查学生书写汉字的能力,从八年级800名学生中随机抽选了50名学生参加测试,这50名学生同时听写50个常用汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出不完整的频数分布表和频数分布直方图如图表:
某校为了调查学生书写汉字的能力,从八年级800名学生中随机抽选了50名学生参加测试,这50名学生同时听写50个常用汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出不完整的频数分布表和频数分布直方图如图表:频数分布表
| 组别 | 成绩x分 | 频数(人数) |
| 第1组 | 25≤x<30 | 4 |
| 第2组 | 30≤x<35 | 8 |
| 第3组 | 35≤x<40 | 16 |
| 第4组 | 40≤x<45 | a |
| 第5组 | 45≤x<50 | 10 |
(1)求表中a的值;
(2)请把频数分布直方图补充完整;
(3)若测试成绩不低于40分为优秀,请你估计该校八年级汉字书写优秀的人数?
(4)第一组中的A、B、C、D 四名同学为提高汉字书写能力,分成两组,每组两人进行对抗练习,请用列表法或画树状图的方法,求A与B名同学能分在同一组的概率.
2.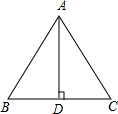 如图,已知AD是△ABC的边BC上的高,下列能使△ABD≌△ACD的条件是( )
如图,已知AD是△ABC的边BC上的高,下列能使△ABD≌△ACD的条件是( )
 如图,已知AD是△ABC的边BC上的高,下列能使△ABD≌△ACD的条件是( )
如图,已知AD是△ABC的边BC上的高,下列能使△ABD≌△ACD的条件是( )| A. | ∠B=45° | B. | ∠BAC=90° | C. | BD=AC | D. | AB=AC |
19.为了估计鱼塘中成品鱼(个体质量在0.5kg及以上,下同)的总质量,先从鱼塘中捕捞50条成品鱼,称得它们的质量如下表:
然后做上记号再放回水库中,过几天又捕捞了100条成品鱼,发现其中2条带有记号.
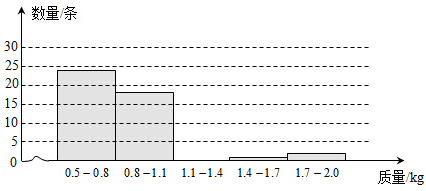
(1)请根据表中数据补全下面的直方图(各组中数据包括左端点不包括右端点).
(2)根据图中数据分组,估计从鱼塘中随机捕一条成品鱼,其质量落在哪一组的可能性最大?
(3)请你用适当的方法估计鱼塘中成品鱼的总质量(精确到1kg).
| 质量/kg | 0.5 | 0.6 | 0.7 | 1.0 | 1.2 | 1.6 | 1.9 |
| 数量/条 | 1 | 8 | 15 | 18 | 5 | 1 | 2 |

(1)请根据表中数据补全下面的直方图(各组中数据包括左端点不包括右端点).
(2)根据图中数据分组,估计从鱼塘中随机捕一条成品鱼,其质量落在哪一组的可能性最大?
(3)请你用适当的方法估计鱼塘中成品鱼的总质量(精确到1kg).
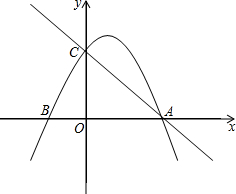 如图,抛物线y=$\frac{1}{k}$(x-2)(x-k)与x轴交于A,B两点,与y轴交于点C.
如图,抛物线y=$\frac{1}{k}$(x-2)(x-k)与x轴交于A,B两点,与y轴交于点C. 小明“六一”去公园玩投掷飞镖的游戏,投中图中阴影部分有奖品(飞镖被平均分成8分).小明能获得奖品的概率是$\frac{5}{8}$.
小明“六一”去公园玩投掷飞镖的游戏,投中图中阴影部分有奖品(飞镖被平均分成8分).小明能获得奖品的概率是$\frac{5}{8}$. 如图所示,在数轴上表示某不等式中的两个不等式的解集,则该不等式组的解集为-2≤x≤1.
如图所示,在数轴上表示某不等式中的两个不等式的解集,则该不等式组的解集为-2≤x≤1.