题目内容
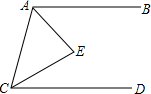
28、如图,AB∥CD,分别探讨下面四个图形中∠APC与∠PAB、∠PCD的关系,请你从所得到的关系中任选一个加以说明.(适当添加辅助线,其实并不难)


分析:关键过转折点作出平行线,根据两直线平行,内错角相等,或结合三角形的外角性质求证即可.
解答:解:如图,

(1)∠APC=∠PAB+∠PCD;
(2)∠APC+∠PAB+∠PCD=360°;
(3)∠APC=∠PAB-∠PCD;
(4)∠APC=∠PCD-∠PAB.
(1)证明:过点P作AB∥PF,所以AB∥CD∥PF,∴∠APC=∠PAB+∠PCD(两直线平行,内错角相等).

(1)∠APC=∠PAB+∠PCD;
(2)∠APC+∠PAB+∠PCD=360°;
(3)∠APC=∠PAB-∠PCD;
(4)∠APC=∠PCD-∠PAB.
(1)证明:过点P作AB∥PF,所以AB∥CD∥PF,∴∠APC=∠PAB+∠PCD(两直线平行,内错角相等).
点评:两直线平行时,应该想到它们的性质,由两直线平行的关系得到角之间的数量关系,从而达到解决问题的目的.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案
相关题目
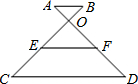 如图,AB∥CD,BO:OC=1:4,点E、F分别是OC、OD的中点,则EF:AB的值为( )
如图,AB∥CD,BO:OC=1:4,点E、F分别是OC、OD的中点,则EF:AB的值为( )| A、1 | B、2 | C、3 | D、4 |
 39、填写推理理由
39、填写推理理由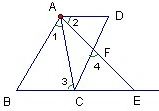 解:∵AB∥CD(已知)
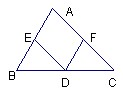
解:∵AB∥CD(已知)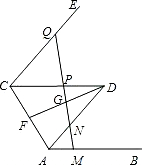 如图,AB∥CD、AD∥CE,F、G分别是AC和FD的中点,过G的直线依次交AB、AD、CD、CE于点M、N、P、Q,
如图,AB∥CD、AD∥CE,F、G分别是AC和FD的中点,过G的直线依次交AB、AD、CD、CE于点M、N、P、Q,