题目内容
若|a+2|+
=0,则在函数y=
中,自变量x的取值范围是( )
| b-1 |
| x+ab |
| A、x>2 | B、x≥2 |
| C、x>-2 | D、x≥-2 |
考点:函数自变量的取值范围
专题:
分析:根据非负数的性质列式求出a、b,再根据被开方数大于等于0列式计算即可得解.
解答:
解:由题意得,a+2=0,b-1=0,
解得a=-2,b=1,
所以,y=
=
,
所以x-2≥0,
解得x≥2.
故选B.
解得a=-2,b=1,
所以,y=
| x+ab |
| x-2 |
所以x-2≥0,
解得x≥2.
故选B.
点评:本题考查了函数自变量的范围,一般从三个方面考虑:
(1)当函数表达式是整式时,自变量可取全体实数;
(2)当函数表达式是分式时,考虑分式的分母不能为0;
(3)当函数表达式是二次根式时,被开方数非负.
(1)当函数表达式是整式时,自变量可取全体实数;
(2)当函数表达式是分式时,考虑分式的分母不能为0;
(3)当函数表达式是二次根式时,被开方数非负.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
某中学书法兴趣小组12名成员的年龄情况如下:
则这个小组成员年龄的众数和中位数分别是( )
| 年龄(岁) | 12 | 13 | 14 | 15 | 16 |
| 人数 | 1 | 4 | 3 | 2 | 2 |
| A、13,14 |
| B、13,15 |
| C、14,14 |
| D、15,16 |
下列结论错误的是( )
| A、sin60°-sin30°=sin30° | ||
| B、sin30°=cos60° | ||
C、tan60°=
| ||
| D、sin245°+cos245°=1 |
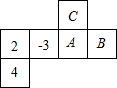 如图是一个正方体的展开图,若正方体相对的面上的两个数互为相反数,则A,B,C三个数依次是( )
如图是一个正方体的展开图,若正方体相对的面上的两个数互为相反数,则A,B,C三个数依次是( )| A、-2,-4,3 |
| B、3,-2,-4 |
| C、-2,3,-4 |
| D、3,-4,-2 |
 用代数式表示图中阴影部分的面积,并计算当x=3时阴影部分的面积.
用代数式表示图中阴影部分的面积,并计算当x=3时阴影部分的面积. 如图,∠3=∠4,试说明:∠1+∠2=180°.
如图,∠3=∠4,试说明:∠1+∠2=180°. 如图,AB∥CD,直线EF与AB、CD相交于点E、F,若∠1=60°,则∠2的度数是
如图,AB∥CD,直线EF与AB、CD相交于点E、F,若∠1=60°,则∠2的度数是