题目内容
 如图,矩形OABC的面积为
如图,矩形OABC的面积为 ,它的对角线OB与双曲线
,它的对角线OB与双曲线 相交于点D,且OB:OD=5:3,则k=________.
相交于点D,且OB:OD=5:3,则k=________.
12
分析:过D作DM⊥OA于M,DN⊥OC于N,设D的坐标是(x,y),根据矩形的性质和平行线分线段成比例定理求出DM= AB,DN=
AB,DN= BC,代入矩形的面积即可求出答案.
BC,代入矩形的面积即可求出答案.
解答:过D作DM⊥OA于M,DN⊥OC于N,
设D的坐标是(x,y),
则DM=y,DN=x,
∵OB:OD=5:3,矩形OABC,
∴∠BAO=90°,
∵DM⊥OA,
∴DM∥BA,
∴△ODM∽△OBA,
∴ =
= =
= ,
,
∴DM= AB,
AB,
同理DN= BC,
BC,
∵四边形OABC的面积为 ,
,
∴AB×BC= ,
,
∴DM×DN=xy= AB×
AB× BC=
BC= ×
× =12,
=12,
即k=xy=12.
故答案为:12.
点评:本题主要考查对矩形的性质,平行线分线段成比例定理,用待定系数法求反比例函数的解析式等知识点的理解和掌握,能推出DM= AB和DN=
AB和DN= BC是解此题的关键.
BC是解此题的关键.
分析:过D作DM⊥OA于M,DN⊥OC于N,设D的坐标是(x,y),根据矩形的性质和平行线分线段成比例定理求出DM=
 AB,DN=
AB,DN= BC,代入矩形的面积即可求出答案.
BC,代入矩形的面积即可求出答案.解答:过D作DM⊥OA于M,DN⊥OC于N,
设D的坐标是(x,y),
则DM=y,DN=x,
∵OB:OD=5:3,矩形OABC,
∴∠BAO=90°,
∵DM⊥OA,
∴DM∥BA,

∴△ODM∽△OBA,
∴
 =
= =
= ,
,∴DM=
 AB,
AB,同理DN=
 BC,
BC,∵四边形OABC的面积为
 ,
,∴AB×BC=
 ,
,∴DM×DN=xy=
 AB×
AB× BC=
BC= ×
× =12,
=12,即k=xy=12.
故答案为:12.
点评:本题主要考查对矩形的性质,平行线分线段成比例定理,用待定系数法求反比例函数的解析式等知识点的理解和掌握,能推出DM=
 AB和DN=
AB和DN= BC是解此题的关键.
BC是解此题的关键. 
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,矩形OABC的顶点0、B的坐标分别是O(0,0)、B(8,4),顶点A在x轴上,顶点C在y轴上,把△OAB沿OB翻折,使点A落在点D的位置,BD与OA交于E.
如图,矩形OABC的顶点0、B的坐标分别是O(0,0)、B(8,4),顶点A在x轴上,顶点C在y轴上,把△OAB沿OB翻折,使点A落在点D的位置,BD与OA交于E.
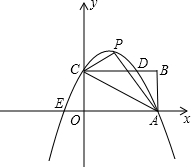 已知如图,矩形OABC的长OA=
已知如图,矩形OABC的长OA= (2013•樊城区模拟)已知如图,矩形OABC的长OA=2
(2013•樊城区模拟)已知如图,矩形OABC的长OA=2 如图,矩形OABC的顶点坐标分别是(0,0),(4,0),(4,1),(0,1),在矩形OABC的内部任取一点(x,y),则x<y的概率是
如图,矩形OABC的顶点坐标分别是(0,0),(4,0),(4,1),(0,1),在矩形OABC的内部任取一点(x,y),则x<y的概率是