Question

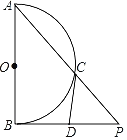
【题目】如图，已知AB为半圆O的直径，过点B作PB⊥OB，连接AP交半圆O于点C，D为BP上一点，CD是半圆O的切线．

（1）求证：CD＝DP．

（2）已知半圆O的直径为，PC＝1，求CD的长．

Answer 1

【答案】（1）证明见解析，（2）CD＝．

【解析】

（1）如图1（见解析），连接OC，先根据圆的切线的性质得出，从而可得，再根据直角三角形的性质可得，然后根据等腰三角形的性质可得，从而可得，最后根据等腰三角形的性质即可得证；

（2）如图2（见解析），连接OC、BC，先根据圆周角定理得出，再根据相似三角形的判定与性质可得，从而可求出，然后在中利用勾股定理可求出，最后根据角的和差、等腰三角形的性质可得，结合题（1）的结论可得，由此即可得．

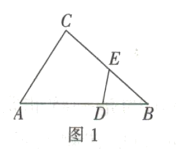
（1）如图1，连接OC

∵CD是半圆O的切线

∴OC⊥CD，即

∴

∵PB⊥AB

∴

∴

又

∴

∴；

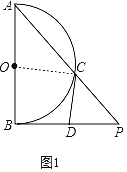
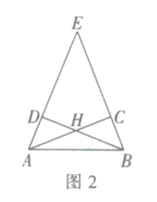
（2）如图2，连接OC、BC

∵AB是半圆O的直径

∴，

∴

又∵

∴

∴，即

∵

∴

解得或（不符题意，舍去）

∴

在中，

由（1）得

即

∵

∴

∴

∴

由（1）知

∴．