题目内容
20. 如图,PA,PB切⊙O于A,B两点,CD切⊙O于点E,交PA,PB于C,D.若⊙O的半径为1,△PCD的周长等于2$\sqrt{3}$,则线段AB的长是( )
如图,PA,PB切⊙O于A,B两点,CD切⊙O于点E,交PA,PB于C,D.若⊙O的半径为1,△PCD的周长等于2$\sqrt{3}$,则线段AB的长是( )| A. | $\sqrt{3}$ | B. | 3 | C. | 2$\sqrt{3}$ | D. | 3$\sqrt{3}$ |
分析 直接利用切线长定理得出AC=EC,DE=DB,PA=PB,进而求出PA的长,然后判定三角形APB为等边三角形即可确定AB的长.
解答 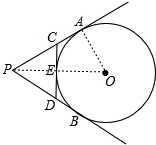 解:∵PA,PB切⊙O于A、B两点,CD切⊙O于点E,交PA,PB于C,D,
解:∵PA,PB切⊙O于A、B两点,CD切⊙O于点E,交PA,PB于C,D,
∴AC=EC,DE=DB,PA=PB,
∵△PCD的周长等于3,
∴PA+PB=2$\sqrt{3}$,
∴PA=PB=$\sqrt{3}$,
链接PA和AO,
∵⊙O的半径为1,
∴sin∠APO=$\frac{AO}{PO}$=$\frac{1}{\sqrt{3}}$=$\frac{\sqrt{3}}{3}$,
∴∠APO=30°,
∴∠APB=60°,
∴△APB是等边三角形,
∴AB=PA=PB=$\sqrt{3}$.
故选:A.
点评 此题主要考查了切线长定理及解直角三角形的知识,熟练应用切线长定理是解题关键.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
10.下列各分式的化简正确的是( )
| A. | $\frac{{x}^{6}}{{x}^{3}}$=x3 | B. | $\frac{a+x}{b+x}$=$\frac{a}{b}$ | C. | $\frac{{x}^{2}}{{x}^{2}}$=0 | D. | $\frac{{a}^{2}-1}{a-1}$=a-1 |
11.如图,把边长为$\sqrt{2}$的正方形的局部进行图①-图④的变换,拼成图⑤,则图⑤的面积是( )


| A. | 8 | B. | 12 | C. | 16 | D. | 18 |
15.已知无论x取何值,y总是取y1=x+1与y2=-2x+4中的最小值,则y的最大值为( )
| A. | 4 | B. | 2 | C. | 1 | D. | 0 |
5.$\sqrt{9}$的值是( )
| A. | 9 | B. | ±3 | C. | 3 | D. | -3 |
12.已知a>b,则下列不等式正确的是( )
| A. | -3a>-3b | B. | a-3>b-3 | C. | 3-a>3-b | D. | ac>bc |
9.检查某产品,合格产品数随抽查的产品总数的变化情况如表:
(1)求出表中空白处的各频率;
(2)从该产品中任抽取一件,抽到的合格产品的概率是多少?
(3)如果任抽取2000件,其中不合格产品约有多少件?
| 抽查产品总数(n) | 50 | 100 | 200 | 500 | 1000 |
| 合格产品数(m) | 48 | 92 | 196 | 485 | 975 |
| 合格产品数与抽查数之比($\frac{m}{n}$) |
(2)从该产品中任抽取一件,抽到的合格产品的概率是多少?
(3)如果任抽取2000件,其中不合格产品约有多少件?