题目内容
【题目】(2017湖南省益阳市)在平面直角坐标系中,将一点(横坐标与纵坐标不相等)的横坐标与纵坐标互换后得到的点叫这一点的“互换点”,如(﹣3,5)与(5,﹣3)是一对“互换点”.
(1)任意一对“互换点”能否都在一个反比例函数的图象上?为什么?
(2)M、N是一对“互换点”,若点M的坐标为(m,n),求直线MN的表达式(用含m、n的代数式表示);
(3)在抛物线![]() 的图象上有一对“互换点”A、B,其中点A在反比例函数
的图象上有一对“互换点”A、B,其中点A在反比例函数![]() 的图象上,直线AB经过点P(
的图象上,直线AB经过点P(![]() ,
,![]() ),求此抛物线的表达式.
),求此抛物线的表达式.
【答案】(1)不一定;(2)y=﹣x+m+n;(3)![]() .
.
【解析】试题分析:(1)设这一对“互换点”的坐标为(a,b)和(b,a).①当ab=0时,它们不可能在反比例函数的图象上,②当ab≠0时,由b=![]() 可得a=
可得a=![]() ,于是得到结论;
,于是得到结论;
(2)把M(m,n),N(n,m)代入y=cx+d,即可得到结论;
(3)设点A(p,q),则q=![]() ,由直线AB经过点P(
,由直线AB经过点P(![]() ,
,![]() ),得到p+q=1,得到q=﹣1或q=2,将这一对“互换点”代入
),得到p+q=1,得到q=﹣1或q=2,将这一对“互换点”代入![]() ,于是得到结论.
,于是得到结论.
试题解析:解:(1)不一定,设这一对“互换点”的坐标为(a,b)和(b,a).
①当ab=0时,它们不可能在反比例函数的图象上,②当ab≠0时,由b=![]() 可得a=
可得a=![]() ,即(a,b)和(b,a)都在反比例函数
,即(a,b)和(b,a)都在反比例函数![]() (k≠0)的图象上;
(k≠0)的图象上;
(2)由M(m,n)得N(n,m),设直线MN的表达式为y=cx+d(c≠0).
则有:![]() ,解得:
,解得:![]() ,∴直线MN的表达式为y=﹣x+m+n;
,∴直线MN的表达式为y=﹣x+m+n;
(3)设点A(p,q),则q=![]() ,∵直线AB经过点P(
,∵直线AB经过点P(![]() ,
,![]() ),由(2)得:
),由(2)得:![]() ,∴p+q=1,∴
,∴p+q=1,∴![]() ,解并检验得:p=2或p=﹣1,∴q=﹣1或q=2,∴这一对“互换点”是(2,﹣1)和(﹣1,2),将这一对“互换点”代入
,解并检验得:p=2或p=﹣1,∴q=﹣1或q=2,∴这一对“互换点”是(2,﹣1)和(﹣1,2),将这一对“互换点”代入![]() 得,∴
得,∴![]() ,解得:
,解得:![]() ,∴此抛物线的表达式为
,∴此抛物线的表达式为![]() .
.

【题目】如图,五边形![]() 内部有若干个点,用这些点以及五边形
内部有若干个点,用这些点以及五边形![]() 的顶点
的顶点![]() 的顶点把原五边形分割成一些三角形(互相不重叠):
的顶点把原五边形分割成一些三角形(互相不重叠):

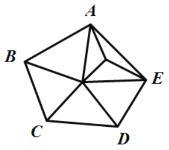
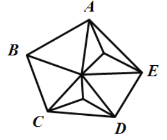
内部有1个点 内部有2个点 内部有3个点
(1)填写下表:
五边形 | 1 | 2 | 3 | 4 | … | n |
分割成的三角形的个数 | 5 | 7 | 9 | … |
(2)原五边形能否被分割成2019个三角形?若能,求此时五边形![]() 内部有多少个点?若不能,请说明理由.
内部有多少个点?若不能,请说明理由.
【题目】有20筐白菜,以每筐30千克为标准,超过或不足的分别用正、负来表示,记录如下:
与标准质量的差(单位:千克) | -3 | -2 | -1.5 | 0 | 1 | 2.5 |
筐数 | 1 | 4 | 2 | 3 | 2 | 8 |
(1)20筐白菜中,最重的一筐比最轻的一筐要重多少千克?
(2)与标准质量比较,20筐白菜总计超过或不足多少千克?
(3)若白菜每千克售价2元,则出售这20筐白菜可卖多少元?



