题目内容
7．解不等式组，并把解集在数轴上表示出来．$\left\{\begin{array}{l}{\frac{x-3}{4}+6≥x①}\\{4-5（x-2）＜8-2x②}\end{array}\right.$．
分析 分别求出每一个不等式的解集，再根据“大于向右，小于向左，包括端点用实心，不包括端点用空心”的原则在数轴上将解集表示出来，继而可得不等式组的解集．
解答 解：解不等式①，得：x≤7，
解不等式②，得：x＞2，
在数轴上表示出不等式的解集如下：
∴不等式组的解集为：2＜x≤7．
点评 本题考查的是解一元一次不等式组，正确求出每一个不等式解集是基础，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键．
练习册系列答案
相关题目
如图，在6×6的正方形网格中（每个小正方形的边长均为1）有一条线段AB，其端点A、B均在格点上，请按要求作图并计算：
15．
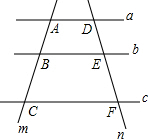如图，直线a∥b∥c，直线m、n分别交直线a、b、c于点A、B、C、D、E、F，若AB=2，CB=DE=3，则线段EF的长为（ ）
如图，直线a∥b∥c，直线m、n分别交直线a、b、c于点A、B、C、D、E、F，若AB=2，CB=DE=3，则线段EF的长为（ ）| A． | $\frac{2}{7}$ | B． | 4 | C． | $\frac{9}{2}$ | D． | 5 |
2．若点（1，-3）在反比例函数y=$\frac{k}{x}$的图象上，则k的值是（ ）
| A． | $\frac{1}{3}$ | B． | 3 | C． | -$\frac{1}{3}$ | D． | -3 |
港口A、B、C依次在同一条直线上，甲、乙两艘船同时分别从A、B港出发，沿该直线匀速驶向C港，甲、乙两船与B港的距离y（千米）与行驶的时间x（h）间的函数关系如图，今有如下说法：①甲船的平均速度为60千米/时；②乙船的平均速度为30千米/时；③甲、乙两船途中相遇两次；④A、B两港之间的距离为30千米，⑤A、C两港之间的距离为90千米，其中正确的有（ ）
19．函数y=-x+1的图象经过的象限是（ ）
| A． | 一、二、三 | B． | 一、二、四 | C． | 一、三、四 | D． | 二、三、四 |
