题目内容
 如图,△ACB、△CDE为等腰直角三角形,∠CAB=∠CDE=90°,F为BE的中点,求证:AF⊥DF,AF=DF.
如图,△ACB、△CDE为等腰直角三角形,∠CAB=∠CDE=90°,F为BE的中点,求证:AF⊥DF,AF=DF.考点:直角三角形斜边上的中线,等腰三角形的判定与性质
专题:证明题
分析:根据直角三角形斜边上的中线等于斜边的一半可得AF=BF=
AE,DF=BF=
AE,再根据等边对等角可得∠ABF=∠BAF,∠DBF=∠BDF,然后根据三角形的一个外角等于与它不相邻的两个内角的和求出∠AFD=2∠ABC,再根据等腰直角三角形的性质求解即可.
| 1 |
| 2 |
| 1 |
| 2 |
解答:证明:∵∠CAB=∠CDE=90°,F为BE的中点,
∴AF=BF=
AE,DF=BF=
AE,
∴AF=DF,
∴∠ABF=∠BAF,∠DBF=∠BDF,
由三角形的外角性质得,∠AFD=∠ABF+∠BAF+∠DBF+∠BDF=2∠ABC,
∵△ABC是等腰直角三角形,
∴∠ABC=45°,
∴∠AFD=90°,
∴AF⊥DF,
综上所述,AF⊥DF,AF=DF.
∴AF=BF=
| 1 |
| 2 |
| 1 |
| 2 |
∴AF=DF,
∴∠ABF=∠BAF,∠DBF=∠BDF,
由三角形的外角性质得,∠AFD=∠ABF+∠BAF+∠DBF+∠BDF=2∠ABC,
∵△ABC是等腰直角三角形,
∴∠ABC=45°,
∴∠AFD=90°,
∴AF⊥DF,
综上所述,AF⊥DF,AF=DF.
点评:本题考查了直角三角形斜边上的中线等于斜边的一半的性质,等腰直角三角形的性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记各性质是解题的关键.

练习册系列答案
相关题目
下列各选项中的两项是同类项的为( )
A、-ab2与-
| ||
| B、32与-53 | ||
| C、x2与-y2a5 | ||
| D、3xy3与2x2y2 |
单项式-2πx3y2z的系数是( ),次数是( )
| A、-2,7 | B、-2π,5 |
| C、-2,6 | D、-2π,6 |
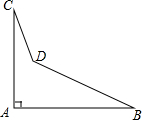 如图,若检验工人量得一个零件的∠A=90°,∠B=32°,∠C=21°,则∠BDC=
如图,若检验工人量得一个零件的∠A=90°,∠B=32°,∠C=21°,则∠BDC=