题目内容
3.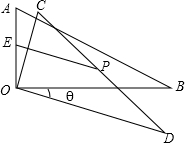 如图,在△AOB中,∠AOB=90°,∠ABO=30°,将△AOB绕顶点O顺时针旋转,旋转角为θ(0°<θ<180°),得到△COD.设AO的中点为E,CD中点为P,AO=a,连接EP,当θ=120°时,EP长度最大,最大值为1.5a.
如图,在△AOB中,∠AOB=90°,∠ABO=30°,将△AOB绕顶点O顺时针旋转,旋转角为θ(0°<θ<180°),得到△COD.设AO的中点为E,CD中点为P,AO=a,连接EP,当θ=120°时,EP长度最大,最大值为1.5a.
分析 根据含30度的直角三角形三边的关系得到AB=2OA=2a,再根据旋转的性质CD=AB=2a,连结OP,根据直角三角形斜边上的中线性质得OP=$\frac{1}{2}$CD,如图1,根据三角形三边的关系得PE<OE+OP,点P、O、E共线时,PE=OE+OP,如图2,点Q为AB的中点,此时PE最大,易得PE的最大值为1.5a,然后求出∠AOP的度数即可得到旋转角的度数.
解答 解:∵∠AOB=90°,∠ABO=30°,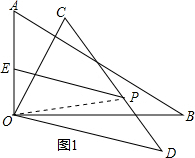
∴AB=2OA=2a,
∵△AOB绕顶点O顺时针旋转,旋转角为θ(0°<<180°)得到△COD,
∴CD=AB=2a,
连结OP,
∵CD中点为P,
∴OP=$\frac{1}{2}$CD=a,
如图1,PE<OE+OP, 点P、O、E共线时,如图2,Q为AB的中点,
点P、O、E共线时,如图2,Q为AB的中点,
∵PE=OE+OP,
∴PE的最大值为0.5a+a=1.5a.
∵QA=QO,
∴∠AOQ=∠A=60°,
∴∠POQ=120°
∴旋转角θ=120°.
故答案为120,1.5a.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了直角三角形斜边上的中线性质.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.二次函数y=15(x-1)2的最小值是( )
| A. | -1 | B. | 1 | C. | 0 | D. | 没有最小值 |
20.圆的面积为$\frac{9}{4}$π,则60°的圆心角所对的弧长是( )
| A. | $\frac{3}{2}$ | B. | $\frac{π}{2}$ | C. | $\frac{\sqrt{6}}{2}$ | D. | $\frac{π}{4}$ |
15.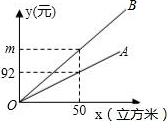 某市发改委举行居民用水价格调整听证会,届时将有两个方案提供听证.如图,射线OA、射线OB分别表示现行的、方案一的每户每月的水费y(元)与每户每月的用水量x(立方米)之间的函数关系,已知方案一的用水价比现行的用水价每立方米多0.96元;
某市发改委举行居民用水价格调整听证会,届时将有两个方案提供听证.如图,射线OA、射线OB分别表示现行的、方案一的每户每月的水费y(元)与每户每月的用水量x(立方米)之间的函数关系,已知方案一的用水价比现行的用水价每立方米多0.96元;
方案二如表所示,每月的每立方米用水价格由该月的用水量决定,其第一、二、三阶的用水价格之比为1:1.5:2(精确到0.01元)
(1)现行的用水量是每立方米1.84元,第三阶的用水价格a=5.22;
(2)求图中m的值和射线OB所对应的函数关系式;
(3)若小明家某月的用水量是a(立方米),请分别写出所提的两种方案下该月的水费b(元)【用含a的代数式表示】
 某市发改委举行居民用水价格调整听证会,届时将有两个方案提供听证.如图,射线OA、射线OB分别表示现行的、方案一的每户每月的水费y(元)与每户每月的用水量x(立方米)之间的函数关系,已知方案一的用水价比现行的用水价每立方米多0.96元;
某市发改委举行居民用水价格调整听证会,届时将有两个方案提供听证.如图,射线OA、射线OB分别表示现行的、方案一的每户每月的水费y(元)与每户每月的用水量x(立方米)之间的函数关系,已知方案一的用水价比现行的用水价每立方米多0.96元;方案二如表所示,每月的每立方米用水价格由该月的用水量决定,其第一、二、三阶的用水价格之比为1:1.5:2(精确到0.01元)
| 阶数 | 用水量(立方米) | 用水价格(元/立方米) |
| 第一阶 | 0~15(含15)的部分 | 2.61 |
| 第二阶 | 15~25(含25)的部分 | 3.92 |
| 第三阶 | 25以上的得分 | n |
(2)求图中m的值和射线OB所对应的函数关系式;
(3)若小明家某月的用水量是a(立方米),请分别写出所提的两种方案下该月的水费b(元)【用含a的代数式表示】
 已知;如图,直线AB不经过点P,请用三角尺或量角器,过点P作直线PD与直线AB垂直,垂足为点D(不写作法,但必须指出并标注所作的直线)
已知;如图,直线AB不经过点P,请用三角尺或量角器,过点P作直线PD与直线AB垂直,垂足为点D(不写作法,但必须指出并标注所作的直线)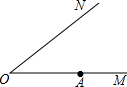 如图,已知ON是一条公路桥梁,现要在上游点A处再建一座与ON平行的大桥AB,请用尺规画出AB方向(不必写作法).并根据你的作法用一句话简单说明为什么AB和ON是平行的?
如图,已知ON是一条公路桥梁,现要在上游点A处再建一座与ON平行的大桥AB,请用尺规画出AB方向(不必写作法).并根据你的作法用一句话简单说明为什么AB和ON是平行的? 如图,AD⊥BC于点D,点E在边AB上,CE与AD交于点G,EF⊥AD于点F,AE=5cm,BE=10cm,BD=9cm,CD=5cm,求AF、FG、GD的长.
如图,AD⊥BC于点D,点E在边AB上,CE与AD交于点G,EF⊥AD于点F,AE=5cm,BE=10cm,BD=9cm,CD=5cm,求AF、FG、GD的长.