题目内容
【题目】某公司在销售一种产品进价为10元的产品时,每年总支出为10万元(不含进货支出).经过若干年销售得知,年销售量![]() (万件)是销售单价
(万件)是销售单价![]() (元)的一次函数,并得到如下部分数据:
(元)的一次函数,并得到如下部分数据:
销售单价 | 12 | 14 | 16 | 18 |
年销售量 | 7 | 6 | 5 | 4 |
(1)求出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)写出该公司销售这种产品的年利润![]() (万元)关于销售单价
(万元)关于销售单价![]() (元)的函数关系式;当销售单价
(元)的函数关系式;当销售单价![]() 为何值时,年利润最大?
为何值时,年利润最大?
(3)试通过(2)中的函数关系式及其大致图象,帮助该公司确定产品的销售单价范围,使年利润不低于20万元(请直接写出销售单价![]() 的范围).
的范围).
【答案】(1)y![]() ;(2)当x=18时,年利润最大;(3)
;(2)当x=18时,年利润最大;(3)![]() .
.
【解析】分析:(1)根据表中的已知点的坐标利用待定系数法确定一次函数的解析式即可;(2)根据总利润=单件利润×销量列出函数关系式,化为顶点式即可确定最值;
(3)令利润大于等于20,求得相应的自变量取值范围,即可解答本题.
本题解析:(1)设y=kx+b,
∵(16,5),(18,4)在此一次函数的图象上,
∴![]() ,
,
解得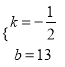 ,
,
故y关于x的函数关系式是:y=![]() x+13;
x+13;
故答案为:y=![]() x+13;
x+13;
(2)∵该公司年利润w=(![]() x+13)(x10)10=
x+13)(x10)10=![]() (x18)+22,
(x18)+22,
∴当x=18时,该公司年利润最大值为22万元,
即该公司销售这种产品的年利润w(万元)关于销售单价x(元)的函数关系式是:
w=![]() (x18)+22,当销售单价x为18时,年利润最大;
(x18)+22,当销售单价x为18时,年利润最大;
(3)年利润不低于20万元时x的取值范围是:16x20,
理由:∵![]() (x18)2+2220
(x18)2+2220
解得:16x20.
即年利润不低于20万元时x的取值范围是:16x20.

练习册系列答案
相关题目








