题目内容
如图所示,已知E是∠AOB的角平分线上一点,EC⊥OA,ED⊥OB,垂足分别为C、D,求证:
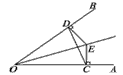
(1)∠ECD=∠EDC;
(2)OC=OD;
(3)OE是CD的垂直平分线
(2)OC=OD;
(3)OE是CD的垂直平分线
解:(1)∵OE平分∠AOB
∴∠DOE=∠COE
∵∠DOE+∠OED=90°,∠OED+∠EDC=90°
∴∠EDC=∠DOE
同理,∠ECD=∠COE
∴∠ECD=∠EDC。
(2)Rt△ODE≌Rt△OCE,OC=OD。
(3)∵DE=EC,∴点E在CD的垂直平分线上
∵OC=OD
∴点O在CD的垂直平分线上
∴OE是CD的垂直平分线。
∴∠DOE=∠COE
∵∠DOE+∠OED=90°,∠OED+∠EDC=90°
∴∠EDC=∠DOE
同理,∠ECD=∠COE
∴∠ECD=∠EDC。
(2)Rt△ODE≌Rt△OCE,OC=OD。
(3)∵DE=EC,∴点E在CD的垂直平分线上
∵OC=OD
∴点O在CD的垂直平分线上
∴OE是CD的垂直平分线。

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案
相关题目
 22、如图所示,已知△ABC是边长为6cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速运动,其中点P运动的速度是1m/s,点Q运动的速度是2m/s,当点Q到达点C时,P、Q两点都停止运动,设运动时间为t s,解答下列问题:
22、如图所示,已知△ABC是边长为6cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速运动,其中点P运动的速度是1m/s,点Q运动的速度是2m/s,当点Q到达点C时,P、Q两点都停止运动,设运动时间为t s,解答下列问题: 19、如图所示,已知O是四边形ABCD内一点,OB=OC=OD,∠BCD=∠BAD=75°,则∠ADO+∠ABO=
19、如图所示,已知O是四边形ABCD内一点,OB=OC=OD,∠BCD=∠BAD=75°,则∠ADO+∠ABO=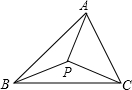 如图所示,已知P是△ABC内一点,试说明PA+PB+PC>
如图所示,已知P是△ABC内一点,试说明PA+PB+PC>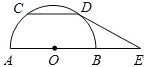 如图所示,已知AB是半圆O的直径,弦CD∥AB,AB=10,CD=6,E是AB延长线上一点,BE=
如图所示,已知AB是半圆O的直径,弦CD∥AB,AB=10,CD=6,E是AB延长线上一点,BE= 20、如图所示,已知AB是半圆O的直径,∠BAC=22°,则∠B=
20、如图所示,已知AB是半圆O的直径,∠BAC=22°,则∠B=