题目内容
18.用一元一次方程的知识解决下面的问题:(1)某商店花500元购进甲、乙两种商品各一件,为获取利润,商店老板决定将甲商品按50%的利润定价,乙商品按40%的利润定价.在实际出售时,应顾客要求,两种商品均按9折出售,这样商店共获利166元,求甲、乙两种商品的进价各是多少元?
(2)某旅行社安排8名旅客分别乘坐两辆小汽车一起赶往飞机场,其中一辆小汽车在距机场15km的地方出了故障.此时,距规定到达机场的时间仅剩42分钟,但唯一可以使用的交通工具只有一辆小汽车,连司机的内限乘坐5人.已知这辆汽车分两批送这8人去机场,平均速度60km/h,现拟如下两种方案:
方案一:小汽车送走第一批人后,第二批人在原地等待汽车返回接送;
方案二:小汽车送走第一批人的同时,第二批人以5km/h的平均速度往机场方向步行,等途中遇返回的汽车时上车前行.
请问这两种方案是否能使这8名旅客在规定的时间内赶到机场?
分析 (1)若设甲商品的进价为x元,乙商品的进价为(500-x)元.根据公式:总利润=总售价-总进价,即可列出方程;
(2)在方案一中,若设小汽车送这两批人到达机场所用的时间为xh,显然根据小汽车所走的总路程是15千米的3倍即可列方程求解.
在方案二中,若设汽车送第一批人返回与第二批人相遇的时间为xh,则此时根据小车和人共走的路程是15千米的2倍,即可列出方程.最后比较所用时间即可.
解答 解:(1)设甲商品的进价为x元,乙商品的进价为(500-x)元,
根据题意得:x•(1+50%)×0.9+90%•(1+40%)(500-x)-500=166,
解得:x=400,则500-x=100.
答:甲商品的进价为400元,乙商品的进价为100元;
(2)方案一:设小汽车送这两批人到达机场所用的时间为xh,
由题意得60x=15×3
解得x=$\frac{3}{4}$,
即$\frac{3}{4}$×60=45min>42min
即:这8名旅客不能在规定的时间内赶到机场.
方案二:设汽车送第一批人返回与第二批人相遇的时间为xh,
则这段时间第二批人走的路程为5xkm,汽车送第二批人用的时间为:$\frac{15-5x}{60}$h,
依题意得:60x+5x=2×15
解得:x=$\frac{6}{13}$,
5x=5×$\frac{6}{13}$=$\frac{30}{13}$,
$\frac{15-5x}{60}$=$\frac{11}{52}$,
所以:汽车送这两批人的时间为$\frac{6}{13}$+$\frac{11}{32}$=$\frac{35}{52}$≈40min<42min.
即:这8名旅客能在规定的时间内赶到机场.
综上所述,采用方案二,这8名旅客能在规定的时间内赶到机场.
点评 本题考查了一元一次方程的应用.解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系列出方程,再求解.

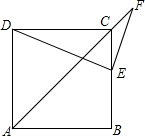 如图,正方形ABCD的边长为10+5$\sqrt{2}$,点E在边CB上,点F在AC的延长线上,EF⊥DE.若CE=CF,则CE的值为( )
如图,正方形ABCD的边长为10+5$\sqrt{2}$,点E在边CB上,点F在AC的延长线上,EF⊥DE.若CE=CF,则CE的值为( )| A. | 5 | B. | 5$\sqrt{2}$ | C. | 10 | D. | 10$\sqrt{2}$ |
| A. | c>a>b | B. | c>b>a | C. | a>c>b | D. | a>b>c |