题目内容
已知矩形的两条对角线的夹角为60°，两条对角线的和为8，则矩形的周长为
- A.2+4
- B.
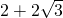
- C.
- D.
C
分析：根据矩形的对角线相等，先求得一条对角线的长，再根据矩形的两条对角线的夹角为60°，求出较短的边等于2，由勾股定理求出较长的边等于2，然后求其周长．
解答：
解：如图，∵AC+BD=8，∴AC=BD=4，
∵∠AOB=60°，∴∠ACB=30°，OA=OB=AB=2，
∴由勾股定理得：BC=
=
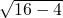=2，
∴矩形的周长=2（2+2）=4+4，
故选C．
点评：本题考查了矩形的对角线平分、相等的性质，还考查了勾股定理的内容．
分析：根据矩形的对角线相等，先求得一条对角线的长，再根据矩形的两条对角线的夹角为60°，求出较短的边等于2，由勾股定理求出较长的边等于2
，然后求其周长．解答：
解：如图，∵AC+BD=8，∴AC=BD=4，∵∠AOB=60°，∴∠ACB=30°，OA=OB=AB=2，
∴由勾股定理得：BC=
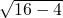==2，∴矩形的周长=2（2+2
）=4+4，故选C．
点评：本题考查了矩形的对角线平分、相等的性质，还考查了勾股定理的内容．
练习册系列答案
全优冲刺100分系列答案
英才点津系列答案
红果子三级测试卷系列答案
相关题目
已知矩形的两条对角线相交所成的一个角为120°，矩形的宽为4cm，则对角线的长为（ ）
| A、2cm | B、4cm | C、8cm | D、16cm |
已知矩形的两条对角线的夹角为60°，两条对角线的和为8，则矩形的周长为（ ）
A、2+4
| ||
B、2+2
| ||
C、4+4
| ||
D、4+2
|
已知矩形的两条对角线相交所成的一个角为120°，矩形的宽为4ｃｍ，则对角线的长为
| A．2ｃｍ | B．4ｃｍ | C．8ｃｍ | D．16ｃｍ |