题目内容
5. 如图,DEFG为△ABC的内接矩形,∠A=90°,D在AB上,G在AC上,EF在斜边BC上,AB=3,AC=4.
如图,DEFG为△ABC的内接矩形,∠A=90°,D在AB上,G在AC上,EF在斜边BC上,AB=3,AC=4.(1)当矩形DEFG周长为$\frac{27}{4}$时,求BE,FC的长.
(2)当S△DEB+S△GFC=$\frac{25}{6}$时,求矩形DEFG的周长.
分析 根据勾股定理得到BC=$\sqrt{A{B}^{2}+A{C}^{2}}$=5,于是得到△ABC三边的比是:AB:AC:BC=3:4:5,根据矩形的性质得到DE=GF,DG∥BC,∠DEF=∠GFC=∠BED=∠GFE=90°,推出△ADG∽△BDE∽△CGF∽△ABC,于是得到△BDE与△CGF与△ADG的相似比都等于3:4:5,
(1)设AD=2x,BD=5y,则DG=5x,DE=4y,BE=3y,GF=DE=4y,CF=$\frac{16}{3}$y,根据已知条件列方程组即可得到结论,
(2)根据已知条件和三角形的面积公式列方程组即可得到结论.
解答 解:∵∠A=90°,AB=3,AC=4,
∴BC=$\sqrt{A{B}^{2}+A{C}^{2}}$=5,
∴△ABC三边的比是:AB:AC:BC=3:4:5,
∵四边形DEFG是矩形,
∴DE=GF,DG∥BC,∠DEF=∠GFC=∠BED=∠GFE=90°,
∴∠AGD=∠C,∠ADG=∠B,
∴△ADG∽△BDE∽△CGF∽△ABC,
∴△BDE与△CGF与△ADG的相似比都等于3:4:5,
(1)设AD=2x,BD=5y,则DG=5x,DE=4y,BE=3y,GF=DE=4y,CF=$\frac{16}{3}$y,
∴$\left\{\begin{array}{l}{3x+5y=3}\\{5x+4y=\frac{27}{8}}\end{array}\right.$,解得:x=y=$\frac{3}{8}$,
∴BE=3y=$\frac{9}{8}$,CF=$\frac{16}{3}$y=2;
(2)∵AB=3,
设AD=2x,BD=5y,则DG=5x,DE=4y,BE=3y,
∴$\left\{\begin{array}{l}{3x+5y=3}\\{\frac{1}{2}×3y•4y+\frac{1}{2}×4y•\frac{16}{3}y=\frac{25}{6}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=\frac{1}{6}}\\{y=\frac{1}{2}}\end{array}\right.$,
∴矩形DEFG的周长=2(5x+4y)=6.
点评 本题考查了相似三角形的判定和性质,矩形的性质,求三角形的面积和矩形的周长,正确的识别图形是解题的关键.

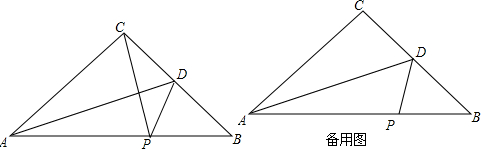
 如图,在△ABC中,AB=3,AC=5,AD是边BC上的中线,AD=ED=2,求△ABC的面积.
如图,在△ABC中,AB=3,AC=5,AD是边BC上的中线,AD=ED=2,求△ABC的面积.