题目内容
探究规律:我们有可以直接应用的结论:若两条直线平行,那么在一条直线上任取一点,无论这点在直线的什么位置,这点到另一条直线的距离均相等.例如:如图1,两直线











如图2,已知直线







(1)请写出图中面积相等的各对三角形: .
(2)如果







解决问题:
如图3,五边形


(1)写出设计方案,并在图4中画出相应的图形;
(2)说明方案设计理由.
练习册系列答案
相关题目




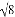 是一个最简二次根式
是一个最简二次根式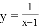 的自变量x的取值范围是x>1 D. 在平面直角坐标系中,点P(2,3)与点Q(﹣2,3)关于y轴对称
的自变量x的取值范围是x>1 D. 在平面直角坐标系中,点P(2,3)与点Q(﹣2,3)关于y轴对称 ,
,




 ,该不等式组的最大整数解是( )
,该不等式组的最大整数解是( )