Question

在△DEF中，DE=DF，点B在EF边上，且∠EBD=60°，C是射线BD上的一个动点（不与点B重合，且BC≠BE），在射线BE上截取BA=BC，连接AC．

（1）当点C在线段BD上时，

①若点C与点D重合，请根据题意补全图1，并直接写出线段AE与BF的数量关系为        ；

②如图2，若点C不与点D重合，请证明AE=BF+CD；

（2）当点C在线段BD的延长线上时，用等式表示线段AE ，BF ，CD之间的数量关系（直接写出结果，不需要证明）．

 

Answer 1

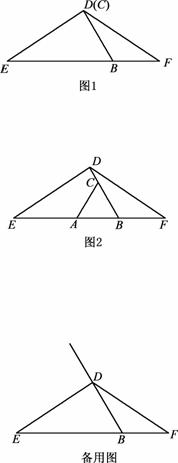（1）①如图：                                 

 

      

AE=BF.         

②证明：在BE上截取BG=BD，连接DG.

            ∵∠EBD=，BG=BD,

            ∴△GBD是等边三角形.

     　　　　同理，△ABC也是等边三角形.

           　∴AG=CD.     

∵DE=DF，∴∠E=∠F.

又∵∠DGB=∠DBG=，

∴∠DGE=∠DBF=.

     　　　　∴△DGE≌△DBF.

∴GE=BF .    

∴AE=BF+CD.

（2）AE=BF－CD或AE=CD－BF .