题目内容
点P为线段AB的中点,分别过线段AB的端点A、B作直线l的垂线,垂足分别为点C、D,连接PC、PD.
(1)当直线l过线段AB的中点P,如图1,猜想PC、PD的数量关系(直接写出你的猜想);
(2)当直线l过线段AB上的任一点,如图2,猜想PC、PD的数量关系并加以证明;
(3)当直线l过线段AB的延长线上的任一点,按照题意画出图形,并判断△PCD的形状(不必证明).

(1)当直线l过线段AB的中点P,如图1,猜想PC、PD的数量关系(直接写出你的猜想);
(2)当直线l过线段AB上的任一点,如图2,猜想PC、PD的数量关系并加以证明;
(3)当直线l过线段AB的延长线上的任一点,按照题意画出图形,并判断△PCD的形状(不必证明).

分析:(1)PC=PD,理由为:由AC与BD都与直线l垂直,利用垂直的定义得到一对直角相等,再由P为AB的中点,得到AP=BP,由对顶角相等得到一对角相等,利用AAS可得出三角形ACP与三角形BDP全等,由全等三角形的对应边相等可得出PC=PD;
(2)PC=PD,理由为:延长CP,交BD于点E,由AC与BD都与直线l垂直,得到AC与BD平行,利用两直线平行内错角相等得到一对角相等,由P为AB的中点,得到AP=BP,再由一对对顶角相等,利用ASA得到三角形ACP与三角形BEP全等,由全等三角形的对应边相等得到P为CE的中点,利用直角三角形中斜边上的中线等于斜边的一半,即可得到CP=DP;
(3)作出相应的图形,如图所示,△PCD为等腰三角形,理由为:延长DP与CA的延长线交于M点,利用AAS得到三角形APM与三角形BPD全等,可得出直角三角形CMD中斜边MD的中点,利用直角三角形斜边上的中线等于斜边的一半可得出PD=PC,即△PCD为等腰三角形.
(2)PC=PD,理由为:延长CP,交BD于点E,由AC与BD都与直线l垂直,得到AC与BD平行,利用两直线平行内错角相等得到一对角相等,由P为AB的中点,得到AP=BP,再由一对对顶角相等,利用ASA得到三角形ACP与三角形BEP全等,由全等三角形的对应边相等得到P为CE的中点,利用直角三角形中斜边上的中线等于斜边的一半,即可得到CP=DP;
(3)作出相应的图形,如图所示,△PCD为等腰三角形,理由为:延长DP与CA的延长线交于M点,利用AAS得到三角形APM与三角形BPD全等,可得出直角三角形CMD中斜边MD的中点,利用直角三角形斜边上的中线等于斜边的一半可得出PD=PC,即△PCD为等腰三角形.
解答:解:(1)PC=PD,理由为:
∵AC⊥l,BD⊥l,
∴∠ACP=∠BDP=90°,
∵P为AB的中点,∴AP=BP,
在△ACP和△BDP中,
,
∴△ACP≌△BDP(AAS),
∴PC=PD;
 (2)如图2所示,延长CP,交BD于点E,
(2)如图2所示,延长CP,交BD于点E,
∵AC⊥l,BD⊥l,
∴∠ACD=∠BDC=90°,
∴AC∥BD,
∴∠A=∠B,
又P为AB的中点,
∴AP=BP,
在△APC和△BPE中,
,
∴△APC≌△BPE(ASA),
∴CP=EP,
在Rt△CDE中,DP为斜边CE上的中线,
则DP=PC=
CE;
 (3)如图,△PCD为等腰三角形,理由如下:
(3)如图,△PCD为等腰三角形,理由如下:
延长DP与CA的延长线交于M点,
∵AC⊥l,BD⊥l,
∴∠ACD=∠BDC=90°,
∴AC∥BD,
∴∠M=∠BDP,
又P为AB的中点,
∴AP=BP,
在△APM和△BPD中,
,
∴△APM≌△BPD(AAS),
∴MP=DP,即P为MD的中点,
在Rt△CDM中,CP=PD=
DM,
则△PCD为等腰三角形.
∵AC⊥l,BD⊥l,
∴∠ACP=∠BDP=90°,
∵P为AB的中点,∴AP=BP,
在△ACP和△BDP中,
|
∴△ACP≌△BDP(AAS),
∴PC=PD;
 (2)如图2所示,延长CP,交BD于点E,
(2)如图2所示,延长CP,交BD于点E,∵AC⊥l,BD⊥l,
∴∠ACD=∠BDC=90°,
∴AC∥BD,
∴∠A=∠B,
又P为AB的中点,
∴AP=BP,
在△APC和△BPE中,
|
∴△APC≌△BPE(ASA),
∴CP=EP,
在Rt△CDE中,DP为斜边CE上的中线,
则DP=PC=
| 1 |
| 2 |
 (3)如图,△PCD为等腰三角形,理由如下:
(3)如图,△PCD为等腰三角形,理由如下:延长DP与CA的延长线交于M点,
∵AC⊥l,BD⊥l,
∴∠ACD=∠BDC=90°,
∴AC∥BD,
∴∠M=∠BDP,
又P为AB的中点,
∴AP=BP,
在△APM和△BPD中,
|
∴△APM≌△BPD(AAS),
∴MP=DP,即P为MD的中点,
在Rt△CDM中,CP=PD=
| 1 |
| 2 |
则△PCD为等腰三角形.
点评:此题考查了全等三角形的判定与性质,直角三角形斜边上的中线性质,以及平行线的判定与性质,作出相应辅助线,构造全等三角形是解本题第2、3问的关键.

练习册系列答案
相关题目
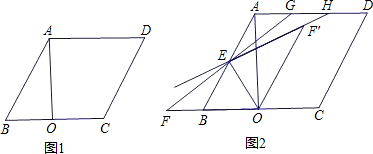
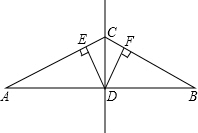 (2013•孝南区一模)如图,点D为线段AB的中点,点C为线段AB的垂直平分线上任意一点,DE⊥AC于点E,DF⊥BC于点F.
(2013•孝南区一模)如图,点D为线段AB的中点,点C为线段AB的垂直平分线上任意一点,DE⊥AC于点E,DF⊥BC于点F. 在等边△ABC中,点E在线段AB上,点D在CB的延长线上,且ED=EC.
在等边△ABC中,点E在线段AB上,点D在CB的延长线上,且ED=EC.