题目内容
 在等边△ABC中,点E在线段AB上,点D在CB的延长线上,且ED=EC.
在等边△ABC中,点E在线段AB上,点D在CB的延长线上,且ED=EC.(1)当点E为线段AB的中点时,试求
|
(2)当点E不是线段AB的中点时,
|
分析:(1)过点E作EF⊥BC于F,设等边三角形的边长为2a,根据等边三角形的性质求出AE,BE的长,再求出∠D=∠BED,根据等角对等边的性质可得BD=BE,然后代入求解,再根据算术平方根的定义求解即可;
(2)过点E作EF⊥BC于F,设BD=x,等边三角形的边长为2a,再根据等腰三角形三线合一的性质表示出CF,然后求出BF,再根据30°角所对的直角边等于斜边的一半求出BE的长度,从而得到AE的长度,然后代入求解,再根据算术平方根的定义解答即可.
(2)过点E作EF⊥BC于F,设BD=x,等边三角形的边长为2a,再根据等腰三角形三线合一的性质表示出CF,然后求出BF,再根据30°角所对的直角边等于斜边的一半求出BE的长度,从而得到AE的长度,然后代入求解,再根据算术平方根的定义解答即可.
解答:解:(1)过点E作EF⊥BC于F,设等边三角形的边长为2a,
∵点E为线段AB的中点,
∴AE=BE=
×2a=a,∠BCE=30°,
∵ED=EC,
∴∠D=∠BCE=30°,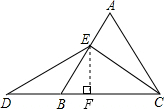
∴∠BED=∠ABC-∠D=60°-30°=30°,
∴BD=BE=a,
=
=
;
(2)不变.理由如下:
过点E作EF⊥BC于F,设BD=x,等边三角形的边长为2a,
∵ED=EC,
∴CF=
CD=
(2a+x),
∴BF=BC-CF=2a-
(2a+x)=a-
x,
在Rt△BEF中,BE=2BF=2a-x,
∴AE=AB-BE=2a-(2a-x)=x,
∴
=
=
.
∵点E为线段AB的中点,
∴AE=BE=
| 1 |
| 2 |
∵ED=EC,
∴∠D=∠BCE=30°,

∴∠BED=∠ABC-∠D=60°-30°=30°,
∴BD=BE=a,
|
|
| 1 |
| 2 |
(2)不变.理由如下:
过点E作EF⊥BC于F,设BD=x,等边三角形的边长为2a,
∵ED=EC,
∴CF=
| 1 |
| 2 |
| 1 |
| 2 |
∴BF=BC-CF=2a-
| 1 |
| 2 |
| 1 |
| 2 |
在Rt△BEF中,BE=2BF=2a-x,
∴AE=AB-BE=2a-(2a-x)=x,
∴
|
|
| 1 |
| 2 |
点评:本题考查了等边三角形的性质,等腰三角形三线合一的性质,算术平方根的定义,直角三角形30°角所对的直角边等于斜边的一半的性质,熟记性质并准确识图,作出辅助线是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
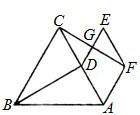 22、如图,在等边△ABC中,点D为AC中点,以AD为边作菱形ADEF,且AF∥BC,连接FC交DE于点G.
22、如图,在等边△ABC中,点D为AC中点,以AD为边作菱形ADEF,且AF∥BC,连接FC交DE于点G.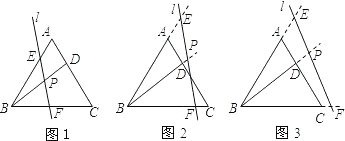 究结果,并说明理由.
究结果,并说明理由.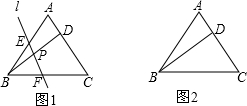
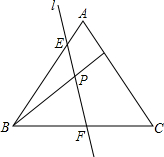 如图,在等边△ABC中,点D为AC上一点,连结AB,BD,BC分别相交于点E,P,F,且∠BPF=60°
如图,在等边△ABC中,点D为AC上一点,连结AB,BD,BC分别相交于点E,P,F,且∠BPF=60° 已知:如图,在等边△ABC中取点P,使得PA,PB,PC的长分别为3,4,5,将线段AP以点A为旋转中心顺时针旋转60°到线段AD,连接BD,下列结论:
已知:如图,在等边△ABC中取点P,使得PA,PB,PC的长分别为3,4,5,将线段AP以点A为旋转中心顺时针旋转60°到线段AD,连接BD,下列结论: