Question

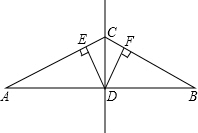（2013•孝南区一模）如图，点D为线段AB的中点，点C为线段AB的垂直平分线上任意一点，DE⊥AC于点E，DF⊥BC于点F．
（1）求证：△CED≌△CFD；
（2）若AB=2a，问当CD为多少时，四边形CEDF为正方形？请说明理由．

Answer 1

分析：（1）由CD垂直平分线AB，可得AC=CB，∴∠ACD=∠BCD，再加∠EDC=∠FDC=90°，可证得△ACD≌△BCD（ASA）；
（2）因为有三个角是直角，且邻边相等的四边形是正方形．所以当CD=

1

2

AB=a时，四边形CEDF为正方形．

解答：（1）证明：∵CD垂直平分线AB，
∴AC=CB．
∵点C为线段AB的垂直平分线上任意一点
∴AC=CB，
∴△ABC是等腰三角形，
∵CD⊥AB，
∴∠ACD=∠BCD．
∵DE⊥AC，DF⊥BC，
∴∠DEC=∠DFC=90°
∴∠EDC=∠FDC，
在△DEC与△DFC中，

∠ACD=∠BCD CD=CD ∠EDC=∠FDC

，
∴△DEC≌△DFC（ASA）；

（2）解：当CD=

1

2

AB=a时，四边形CEDF为正方形．
理由如下：
∵CD⊥AB，
∴∠CDB=∠CDA=90°，
∵CD=

1

2

AB，
∴CD=BD=AD，
∴∠B=∠DCB=∠ACD=45°，
∴∠ACB=90°，
∴四边形ECFD是矩形，
∵CE=CF，
∴四边形ECFD是正方形．

点评：此题主要考查线段的垂直平分线的性质、全等三角形的判定及性质、正方形的判定等知识点．