Question

2．在△ABC所在平面内有一点P，点P到直线AB、AC距离相等，且到B、C两点距离相等．根据以上条件可以画出以下四个图：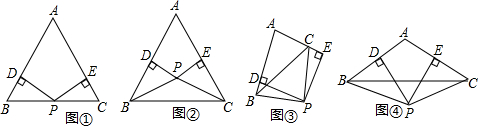

在每个图中均有PD⊥AB，PE⊥AC，D、E为垂足，且PD=PE，PB=PC．
（1）哪几个图能说明△ABC为等腰三角形？请就其中一个图进行说明．
（2）请用尺规作图找到下图中符合上述条件的点P．（不写作法保留作图痕迹）
（3）如图③，若AB=a，AC=b（a＞b），请用含a、b的代数式表示BD的长度．

Answer 1

分析 （1）根据角平分线和线段垂直平分线的性质证明即可；
（2）作出∠A的平分线和BC的中垂线即可；
（3）根据角平分线和线段垂直平分线的性质得出PD=PE，PB=PC，再利用HL证明三角形全等，进而转化解答即可．

解答 解：（1）图①图②图④能说明△ABC为等腰三角形．
如图①，∵PD⊥AB，PE⊥AC，D、E为垂足，PD=PE，
∴AP是三角形BC边上的角平分线，
∵PB=PC，
∴AP是三角形BC边上的中线，
∴△ABC为等腰三角形；
（2）作出∠A的平分线和BC的中垂线，交点即为点P；   
（3）∵点P到直线AB、AC距离相等，且到B、C两点距离相等，
∴PD=PE，PB=PC，
在Rt△DBP与Rt△ECP中，
$\left\{\begin{array}{l}{PD=PE}\\{PB=PC}\end{array}\right.$，
∴Rt△DBP≌Rt△ECP（HL），
∴DB=CE，
∵AD=AE，
∴AB=AC+CE+DB，
即BD=$\frac{AB-AC}{2}$=$\frac{a-b}{2}$．

点评 此题考查作图与设计应用，关键是根据角平分线和线段垂直平分线的作图和性质解答．