题目内容
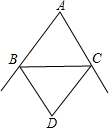 如图,△ABC的两外角平分线相交于点D,∠A=50°,则∠D=
如图,△ABC的两外角平分线相交于点D,∠A=50°,则∠D=分析:根据三角形的内角和定理,得∠D=180°-(∠1+∠2),结合角平分线定义,
得∠1+∠2=
(∠CBE+∠BCF),再根据平角的定义得出∠CBE+∠BCF=180°-∠ABC+180°-∠BCA,就可找到∠D和∠A的关系,从而求解.
得∠1+∠2=
| 1 |
| 2 |
解答: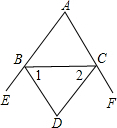 解:根据三角形的内角和定理、角平分线定义以及三角形的外角的性质,得
解:根据三角形的内角和定理、角平分线定义以及三角形的外角的性质,得
∠D=180°-(∠1+∠2)
=180°-
(∠CBE+∠BCF)
=180°-
(180°-∠ABC+180°-∠BCA)
=180°-
(180°+∠A)
=90°-
∠A
=65°.
 解:根据三角形的内角和定理、角平分线定义以及三角形的外角的性质,得
解:根据三角形的内角和定理、角平分线定义以及三角形的外角的性质,得∠D=180°-(∠1+∠2)
=180°-
| 1 |
| 2 |
=180°-
| 1 |
| 2 |
=180°-
| 1 |
| 2 |
=90°-
| 1 |
| 2 |
=65°.
点评:熟记此题的结论便于快速地解决一些填空题或选择题.
三角形的两外角平分线相交所成的锐角等于90°减去不相邻的第三个内角的一半.
三角形的两外角平分线相交所成的锐角等于90°减去不相邻的第三个内角的一半.

练习册系列答案
相关题目
 18、如图,△ABC中,∠ACB=90°,AC=BC,CO为中线.现将一直角三角板的直角顶点放在点O上并绕点O旋转,若三角板的两直角边分别交AC,CB的延长线于点G,H.
18、如图,△ABC中,∠ACB=90°,AC=BC,CO为中线.现将一直角三角板的直角顶点放在点O上并绕点O旋转,若三角板的两直角边分别交AC,CB的延长线于点G,H. (2012•潍坊)如图,三角形ABC的两个顶点B、C在圆上,顶点A在圆外,AB、AC分别交圆于E、D两点,连接EC、BD.
(2012•潍坊)如图,三角形ABC的两个顶点B、C在圆上,顶点A在圆外,AB、AC分别交圆于E、D两点,连接EC、BD.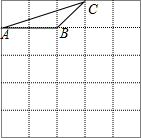 (2011•和平区模拟)在正方形网格中,每个小正方形的顶点称为格点,以格点连线为边的三角形叫做格点三角形,如图,△ABC是格点三角形,请你在给出的5×5的正方形网格中,分别画出与△ABC相似、面积最小的和面积最大的格点三角形(画出的两个三角形及△ABC除顶点和边可以重合外,其余部分不能重合).
(2011•和平区模拟)在正方形网格中,每个小正方形的顶点称为格点,以格点连线为边的三角形叫做格点三角形,如图,△ABC是格点三角形,请你在给出的5×5的正方形网格中,分别画出与△ABC相似、面积最小的和面积最大的格点三角形(画出的两个三角形及△ABC除顶点和边可以重合外,其余部分不能重合). 已知:如图,分别以直角三角形ABC的两直角边AB、BC为一边,向外作等边三角形ABE和等边三角形BCF,连接EF、EC,延长EB交FC于M.
已知:如图,分别以直角三角形ABC的两直角边AB、BC为一边,向外作等边三角形ABE和等边三角形BCF,连接EF、EC,延长EB交FC于M. 如图,以Rt△ABC的两条直角边为边长向外作正方形I、II,若AB=3,则正方形I、II的面积和为
如图,以Rt△ABC的两条直角边为边长向外作正方形I、II,若AB=3,则正方形I、II的面积和为