题目内容
 已知:如图,分别以直角三角形ABC的两直角边AB、BC为一边,向外作等边三角形ABE和等边三角形BCF,连接EF、EC,延长EB交FC于M.
已知:如图,分别以直角三角形ABC的两直角边AB、BC为一边,向外作等边三角形ABE和等边三角形BCF,连接EF、EC,延长EB交FC于M.(1)求∠FBE的度数;
(2)求证:EF=EC;
(3)求证:EM⊥CF.
分析:(1)根据等边三角形的性质得到∠CBF=∠ABE=60°,然后根据周角的定义可计算出∠FBE=360°-∠CBF-∠CBA-∠ABE=150°;
(2)由于∠CBE=∠CBA+∠ABE=60°+90°=150°,结合(1)的结论得到∠FBE=∠CBE,再根据等边三角形的性质得到BF=BC,BE=BA,然后根据“SAS”可判定△BFE≌△BCE,则EF=EC;
(3)由△BFE≌△BCE,则EF=EC,∠FEB=∠CEB,于是BE平分等腰三角形EFC的顶角,根据等腰三角形的三线合一即可得到结论.
(2)由于∠CBE=∠CBA+∠ABE=60°+90°=150°,结合(1)的结论得到∠FBE=∠CBE,再根据等边三角形的性质得到BF=BC,BE=BA,然后根据“SAS”可判定△BFE≌△BCE,则EF=EC;
(3)由△BFE≌△BCE,则EF=EC,∠FEB=∠CEB,于是BE平分等腰三角形EFC的顶角,根据等腰三角形的三线合一即可得到结论.
解答:(1)解:∵△ABE和△BCF都是等边三角形,
∴∠CBF=∠ABE=60°,
而∠CBA=90°,
∴∠FBE=360°-∠CBF-∠CBA-∠ABE=150°;
(2)证明:∵∠CBE=∠CBA+∠ABE=60°+90°=150°,
∴∠FBE=∠CBE,
∵△ABE和△BCF都是等边三角形,
∴BF=BC,BE=BA,
∵在△BFE和△BCE中
,
∴△BFE≌△BCE(SAS),
∴EF=EC;
(3)证明:∵△BFE≌△BCE,
∴EF=EC,∠FEB=∠CEB,
∴BE平分等腰三角形EFC的顶角,
∴EB⊥CF,
即EM⊥CF.
∴∠CBF=∠ABE=60°,
而∠CBA=90°,
∴∠FBE=360°-∠CBF-∠CBA-∠ABE=150°;
(2)证明:∵∠CBE=∠CBA+∠ABE=60°+90°=150°,
∴∠FBE=∠CBE,
∵△ABE和△BCF都是等边三角形,
∴BF=BC,BE=BA,
∵在△BFE和△BCE中
|
∴△BFE≌△BCE(SAS),
∴EF=EC;
(3)证明:∵△BFE≌△BCE,
∴EF=EC,∠FEB=∠CEB,
∴BE平分等腰三角形EFC的顶角,
∴EB⊥CF,
即EM⊥CF.
点评:本题考查了全等三角形的判定与性质:有两组边对应相等,且它们所夹的角也相等,那么这两个三角形全等;全等三角形的对应边相等,对应角相等.也考查了等边三角形的性质以及等腰三角形的性质.

练习册系列答案
相关题目
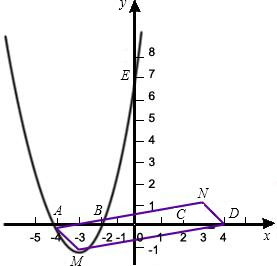 如图,已知抛物线C1与坐标轴的交点依次是A(-4,0),B(-2,0),E(0,8).
如图,已知抛物线C1与坐标轴的交点依次是A(-4,0),B(-2,0),E(0,8). 19、如图所示,在直角坐标系中,矩形OBCD的边长OB=4,OD=2.
19、如图所示,在直角坐标系中,矩形OBCD的边长OB=4,OD=2. 直高度为3.5米,C点与O点的水平距离为7米,以O为坐标原点,水平方向与竖直方向分别为x轴、y轴,建立直角坐标系.
直高度为3.5米,C点与O点的水平距离为7米,以O为坐标原点,水平方向与竖直方向分别为x轴、y轴,建立直角坐标系. 28、如图所示,在直角坐标系中,矩形OBCD的边长OB=4,OD=2.
28、如图所示,在直角坐标系中,矩形OBCD的边长OB=4,OD=2. (2012•咸丰县二模)如图,已知在Rt△ABC中,∠ACB=90°,AB=10,分别以AC、BC为直经作半圆,面积分别记为S1、S2,则S1+S2的值等于( )
(2012•咸丰县二模)如图,已知在Rt△ABC中,∠ACB=90°,AB=10,分别以AC、BC为直经作半圆,面积分别记为S1、S2,则S1+S2的值等于( )