题目内容
对于每个非零自然数n,抛物线y=x2﹣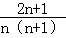 x+
x+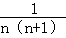 与x轴交于An、Bn两点,以AnBn表示这两点间的距离,则A1B1+A2B2+…+A2015B2015的值是( )
与x轴交于An、Bn两点,以AnBn表示这两点间的距离,则A1B1+A2B2+…+A2015B2015的值是( )
A.1 B.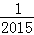 C.
C.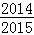 D.
D.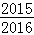
D【考点】抛物线与x轴的交点.
【分析】首先求出抛物线与x轴两个交点坐标,然后由题意得到AnBn= ﹣
﹣ ,进而求出A1B1+A2B2+…+A2015B2015的值.
,进而求出A1B1+A2B2+…+A2015B2015的值.
【解答】解:令y=x2﹣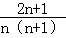 x+
x+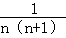 =0,
=0,
即x2﹣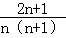 x+
x+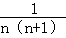 =0,
=0,
解得x= 或x=
或x= ,
,
故抛物线y=x2﹣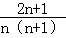 x+
x+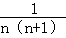 与x轴的交点为(
与x轴的交点为( ,0),(
,0),( ,0),
,0),
由题意得AnBn= ﹣
﹣ ,
,
则A1B1+A2B2+…+A2015B2015=1﹣ +
+ ﹣
﹣ +…+
+…+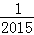 ﹣
﹣ =1﹣
=1﹣ =
=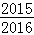 ,
,
故选D.
【点评】本题主要考查了抛物线与x轴交点的知识,解答本题的关键是用n表示出抛物线与x轴的两个交点坐标,此题难度不大.

练习册系列答案
相关题目
 ,求
,求 .
.
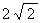 cm,点 P 从点B出发沿BC方向以1cm/s的速度向点C运动,当点P到点C时,停止运动。PQ⊥BC,PQ交AB或AC于点Q,以PQ为一边向右侧作矩形PQRS,PS=2PQ,矩形PQRS与△ABC重叠部分的面积为S(cm2),点P的运动时间为t(s)。回答下列问题:
cm,点 P 从点B出发沿BC方向以1cm/s的速度向点C运动,当点P到点C时,停止运动。PQ⊥BC,PQ交AB或AC于点Q,以PQ为一边向右侧作矩形PQRS,PS=2PQ,矩形PQRS与△ABC重叠部分的面积为S(cm2),点P的运动时间为t(s)。回答下列问题: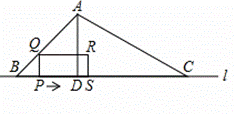

 +3向下平移2个单位后得抛物线y2,则阴影部分的面积S= .
+3向下平移2个单位后得抛物线y2,则阴影部分的面积S= .
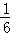 x2+bx+c表示,且抛物线的点C到墙面OB的水平距离为3m时,到地面OA的距离为
x2+bx+c表示,且抛物线的点C到墙面OB的水平距离为3m时,到地面OA的距离为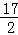 m.
m.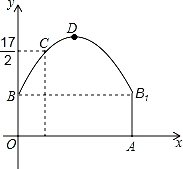
 是一元二次方程
是一元二次方程 的一个根,求
的一个根,求 的值和方程的另一个根.
的值和方程的另一个根. -x4
-x4