题目内容
11. 如图,A处在B处北偏西45°方向,C处在B处北偏东15°方向,C处在A处南偏东80°方向,求∠C的度数.(注:上北,下南,左西,右东)
如图,A处在B处北偏西45°方向,C处在B处北偏东15°方向,C处在A处南偏东80°方向,求∠C的度数.(注:上北,下南,左西,右东)
分析 根据AM∥BN,得到∠MAB=∠ABN=45°,所以∠CAB=∠MAC-∠MAB=80°-45°=35°,在△ABC中,∠C=180°-∠CAB-∠ABN-∠NBC=180°-35°-45°-15°=75°.
解答 解:∵A处在B处北偏西45°方向,C处在B处北偏东15°方向,C处在A处南偏东80°方向,
∴∠ABN=45°,∠NBC=15°,∠CAM=80°,
∵AM∥BN,
∴∠MAB=∠ABN=45°,
∴∠CAB=∠MAC-∠MAB=80°-45°=35°,
在△ABC中,∠C=180°-∠CAB-∠ABN-∠NBC=180°-35°-45°-15°=75°.
点评 本题考查了方向角,利用了方向角,平行线的性质,角的和差,三角形的内角和定理.

练习册系列答案
相关题目
1.若|x-2|+|y-3|=0,则x+y=( )
| A. | ±5 | B. | 5 | C. | ±1 | D. | 1 |
3.下列各组有理数的大小比较中,错误的是( )
| A. | -(-$\frac{1}{5}$)$>-\frac{1}{5}$ | B. | -(-3$\frac{2}{5}$)>(-3$\frac{2}{5}$) | C. | -(-4)<+(+4) | D. | +(-1.1)<0 |
20.小华是一个理财小能手,上周末他数了数白己的零花钱共有120元,下表是小华本周零花钱记录情况,+号表示当天的零花钱有节余,-号表示当天的零花钱超出预算:
(1)请你帮小华算一算,本周小华哪天的零花钱总数最多?哪天的零花钱总数最少?
(2)本周末小华的零花钱总数比上周末多还是少?
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 零花钱 | +3 | -4 | +3 | +2 | +1 | -5 | +5 |
(2)本周末小华的零花钱总数比上周末多还是少?
 如图,在△ABC中,D是BC上一点,AC=15,BC=12,CD=4,在AC上找一点E,使△CDE与△ABC相似,求CE的长.
如图,在△ABC中,D是BC上一点,AC=15,BC=12,CD=4,在AC上找一点E,使△CDE与△ABC相似,求CE的长.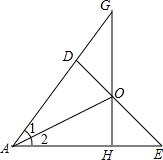 已知,如图,OD⊥AD,OH⊥AE,DE交GH于O.若∠1=∠2,求证:OG=OE.
已知,如图,OD⊥AD,OH⊥AE,DE交GH于O.若∠1=∠2,求证:OG=OE.