题目内容
 如图,AB是⊙O的直径,点C在⊙O上,且CA=CB.将线段AC绕点A逆时针旋转45°得线段AC′.
如图,AB是⊙O的直径,点C在⊙O上,且CA=CB.将线段AC绕点A逆时针旋转45°得线段AC′.
(1)求证:AC′是⊙O的切线;
(2)若AC′=4,求⊙O的半径的长.
(1)证明:∵AB是⊙O直径,
∴∠ACB=90°.
又∵CA=CB,
∴∠CAB=45°.
又∵∠C′AC=45°,
∴∠C′AO=90°,
即OA⊥C′A.
∴AC′是⊙O的切线.
(2)解:∵线段AC绕点A逆时针旋转45°得线段AC′,
∴CA=C′A=4.
在Rt△ACB中,∠CAB=45°,
∵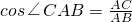 ,
,
∴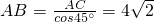 .
.
∴OA= .
.
如有其他解(证)法,请酌情给分.
分析:(1)根据AB为直径,则∠C=90°,由CA=CB,则∠BAC=45°,再根据旋转角等于45°,得出∠BAC′=90度,从而得出AC′是⊙O的切线;
(2)根据勾股定理或三角函数可得出答案.
点评:本题考查了切线的判定和性质,以及勾股定理,是基础知识要熟练掌握.
∴∠ACB=90°.
又∵CA=CB,
∴∠CAB=45°.
又∵∠C′AC=45°,
∴∠C′AO=90°,
即OA⊥C′A.
∴AC′是⊙O的切线.
(2)解:∵线段AC绕点A逆时针旋转45°得线段AC′,
∴CA=C′A=4.
在Rt△ACB中,∠CAB=45°,
∵
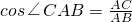 ,
,∴
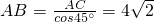 .
.∴OA=
 .
.如有其他解(证)法,请酌情给分.
分析:(1)根据AB为直径,则∠C=90°,由CA=CB,则∠BAC=45°,再根据旋转角等于45°,得出∠BAC′=90度,从而得出AC′是⊙O的切线;
(2)根据勾股定理或三角函数可得出答案.
点评:本题考查了切线的判定和性质,以及勾股定理,是基础知识要熟练掌握.

练习册系列答案
相关题目
 8、如图,AB是铅直地竖立在坡角为30°的山坡上的电线杆,当阳光与水平线成60°角时,电线杆的影子BC的长度为4米,则电线杆AB的高度为( )
8、如图,AB是铅直地竖立在坡角为30°的山坡上的电线杆,当阳光与水平线成60°角时,电线杆的影子BC的长度为4米,则电线杆AB的高度为( ) 0.1平方米)
0.1平方米)

 如图,AB是铅直地竖立在坡角为30°的山坡上的电线杆,当阳光与水平线成60°角时,电线杆的影子BC的长度为4米,则电线杆AB的高度为
如图,AB是铅直地竖立在坡角为30°的山坡上的电线杆,当阳光与水平线成60°角时,电线杆的影子BC的长度为4米,则电线杆AB的高度为