题目内容
△ABC的内切圆⊙I分别切BC、CA、AB于D、E、F,若∠A=70°,则∠EDF=________度.
55
分析:连接IF,IE,可得IE⊥AC,IF⊥AB,又因为∠A=70°,易得∠EIF=110°,则可求得∠EDF.
解答: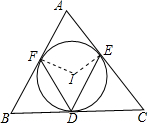 解:连接IF,IE,
解:连接IF,IE,
∵△ABC的内切圆⊙I分别切BC、CA、AB于D、E、F,
∴IE⊥AC,IF⊥AB,
∴∠IFA=∠IEA=90°,
∵∠A=70°,
∴∠EIF=110°,
∴∠EDF=55°.
点评:此题考查了三角形的内切圆的性质与圆周角定理(同弧所对的圆周角等于它所对圆心角的一半).解题的关键是数形结合思想的应用.
分析:连接IF,IE,可得IE⊥AC,IF⊥AB,又因为∠A=70°,易得∠EIF=110°,则可求得∠EDF.
解答:
 解:连接IF,IE,
解:连接IF,IE,∵△ABC的内切圆⊙I分别切BC、CA、AB于D、E、F,
∴IE⊥AC,IF⊥AB,
∴∠IFA=∠IEA=90°,
∵∠A=70°,
∴∠EIF=110°,
∴∠EDF=55°.
点评:此题考查了三角形的内切圆的性质与圆周角定理(同弧所对的圆周角等于它所对圆心角的一半).解题的关键是数形结合思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
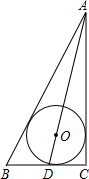 如图,⊙O为△ABC的内切圆,∠C=90度,OA的延长线交BC于点D,AC=4,CD=1,则⊙O的半径等于( )
如图,⊙O为△ABC的内切圆,∠C=90度,OA的延长线交BC于点D,AC=4,CD=1,则⊙O的半径等于( )A、
| ||
B、
| ||
C、
| ||
D、
|
⊙O是△ABC的内切圆,且∠C=90°,切点为D,E,F,若AF,BE的长是方程x2-13x+30=0的两个根,则S△ABC的值为( )
| A、30 | B、15 | C、60 | D、13 |
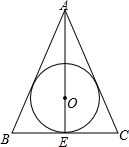 如图,等腰△ABC中,AE是底边BC上的高,点O在AE上,⊙O与AB和BC分别相切.
如图,等腰△ABC中,AE是底边BC上的高,点O在AE上,⊙O与AB和BC分别相切.
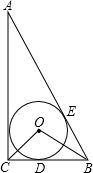 (2013•长宁区一模)如图,已知Rt△ABC中,∠ACB=90°,⊙O 是Rt△ABC的内切圆,其半径为1,E、D是切点,∠BOC=105°.求AE的长.
(2013•长宁区一模)如图,已知Rt△ABC中,∠ACB=90°,⊙O 是Rt△ABC的内切圆,其半径为1,E、D是切点,∠BOC=105°.求AE的长.