题目内容
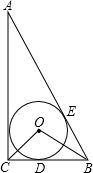 (2013•长宁区一模)如图,已知Rt△ABC中,∠ACB=90°,⊙O 是Rt△ABC的内切圆,其半径为1,E、D是切点,∠BOC=105°.求AE的长.
(2013•长宁区一模)如图,已知Rt△ABC中,∠ACB=90°,⊙O 是Rt△ABC的内切圆,其半径为1,E、D是切点,∠BOC=105°.求AE的长.分析:首先根据切线长的性质以及切线的性质得出BD的长,进而得出BC的长以及AB的长,即可得出AE的长.
解答: 解:连接OD、OE.
解:连接OD、OE.
则OD=OE=1,
∵O是△ABC的内切圆圆心
∴OB、OC分别是∠ABC、∠ACB的角平分线,
即∠OBD=∠OBE=
∠ABC且∠OCD=
∠ACB
又∵∠ACB=90°,∴∠OCD=
∠ACB=45°,
∵OD、OE是过切点的半径,
∴OD⊥BC 且OE⊥AB,∴∠OCD+∠COD=90°,
∴∠COD=∠OCD=45°,∴OD=CD=1,
∵∠COB=105°,∴∠DOB=∠COB-∠COD=60°,
在Rt△OBD中,
tan∠BOD=
=
=
,
∴DB=
,
∠OBD+∠BOD=90°,∴∠OBD=30°,
∵∠DOB=∠OBE=
∠ABC=30°,
∴∠ABC=60°,
∴BC=BD+CD=1+
在Rt△ABC中,
AB=2+2
,
在Rt△OBE中,
∵OE=1,∠OBE=30°,
∴BE=
=
,
∴AE=2+
.
 解:连接OD、OE.
解:连接OD、OE.则OD=OE=1,
∵O是△ABC的内切圆圆心
∴OB、OC分别是∠ABC、∠ACB的角平分线,
即∠OBD=∠OBE=
| 1 |
| 2 |
| 1 |
| 2 |
又∵∠ACB=90°,∴∠OCD=
| 1 |
| 2 |
∵OD、OE是过切点的半径,
∴OD⊥BC 且OE⊥AB,∴∠OCD+∠COD=90°,
∴∠COD=∠OCD=45°,∴OD=CD=1,
∵∠COB=105°,∴∠DOB=∠COB-∠COD=60°,
在Rt△OBD中,
tan∠BOD=
| DB |
| OD |
| DB |
| 1 |
| 3 |
∴DB=
| 3 |
∠OBD+∠BOD=90°,∴∠OBD=30°,
∵∠DOB=∠OBE=
| 1 |
| 2 |
∴∠ABC=60°,
∴BC=BD+CD=1+
| 3 |
在Rt△ABC中,
AB=2+2
| 3 |
在Rt△OBE中,
∵OE=1,∠OBE=30°,
∴BE=
| 1 |
| tan30° |
| 3 |
∴AE=2+
| 3 |
点评:此题主要考查了切线的性质以及锐角三角函数的应用,正确得出∠ABC的度数以及BC的长是解题关键.

练习册系列答案
相关题目
 (2013•长宁区一模)如图,圆O的弦AB垂直平分半径OC,则四边形OACB一定是( )
(2013•长宁区一模)如图,圆O的弦AB垂直平分半径OC,则四边形OACB一定是( )