��Ŀ����
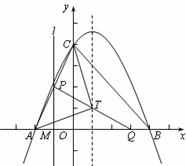
��ͼ�������ߣ�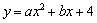 ��
��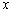 �ύ�ڵ�A(��2��0)��B(4��0)����
�ύ�ڵ�A(��2��0)��B(4��0)����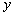 �ύ�ڵ�C��
�ύ�ڵ�C��
(1)�������ߵĽ���ʽ��
(2 )T�������߶Գ����ϵ�һ�㣬�ҡ�ACT����ACΪ�ĵ��������Σ����T�����ꣻ
)T�������߶Գ����ϵ�һ�㣬�ҡ�ACT����ACΪ�ĵ��������Σ����T�����ꣻ
(3)��M��Q�ֱ�ӵ�A��B��ÿ��1����λ���ȵ��ٶ���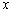 ��ͬʱ����������У�����M��ԭ��ʱ����Q���̵�ͷ����ÿ��
��ͬʱ����������У�����M��ԭ��ʱ����Q���̵�ͷ����ÿ�� ����λ���ȵ��ٶ����B�����ƶ�������M���������ߵĶԳ���ʱ������ֹͣ�˶�������M��ֱ��l���ᣬ��AC��BC�ڵ�P�����M���˶�ʱ��t(��)���APQ�����S�ĺ�����ϵʽ�������S�����ֵ��
����λ���ȵ��ٶ����B�����ƶ�������M���������ߵĶԳ���ʱ������ֹͣ�˶�������M��ֱ��l���ᣬ��AC��BC�ڵ�P�����M���˶�ʱ��t(��)���APQ�����S�ĺ�����ϵʽ�������S�����ֵ��
�⣺��1����A����2��0����B(4��0)����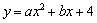 ����
����
 ��
�� ���
��� ��������1��
��������1��
�������ߵĽ���ʽΪ�� �� ��������1��
�� ��������1��
��2���� ���������ߵĶԳ���Ϊֱ��
���������ߵĶԳ���Ϊֱ�� ��
��
ֱ�� ��
��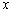 ���ڵ�D����ֱ��
���ڵ�D����ֱ�� ��һ��T(1��
��һ��T(1�� )�� ��������1��
)�� ��������1��
��CE��ֱ�� ������ΪE��
������ΪE��
��C(0��4)�õ�E(1��4)�� ��������1��
��Rt��ADT��Rt��TEC��
��TA��TC�� �� ��������1��
�� ��������1��
��� �����T������Ϊ(1��1). ��������1��
�����T������Ϊ(1��1). ��������1��
��3���⣺���� ʱ����AMP�ס�AOC ��
ʱ����AMP�ס�AOC ��
�� ��
�� �� ��������1��
�� ��������1��
��  ��������1��
��������1��
�ߵ� ʱ��S��
ʱ��S�� �����Ӷ����ӣ�
�����Ӷ����ӣ�
�൱ ʱ��S�����ֵΪ8�� ��������1��
ʱ��S�����ֵΪ8�� ��������1��
���� ʱ����PF��y����F��
ʱ����PF��y����F��
�С�COB�ס�CFP��
��CO��OB��
��FP��FC�� ��
��
 ��������1��
��������1��
�� ��������1��
��������1��
�൱ ʱ��S�����ֵΪ
ʱ��S�����ֵΪ �� ��������1��
�� ��������1��
����������S�����ֵΪ ��
��



��x��y=1��3��2y=3z���� ��ֵ�ǣ�������
��ֵ�ǣ�������
| �� | A�� | ��5 | B�� | �� | C�� |
| D�� | 5 |
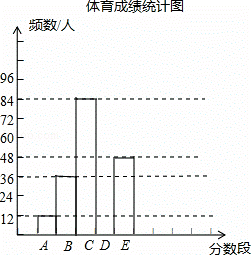
Ϊ���˽�ij�г����꼶ѧ�������ɼ����ɼ���Ϊ�������������ȡ�˲���ѧ���������ɼ����ֶΣ�A��20.5��22.5��B��22.5��24.5��C��24.5��26.5��D��26.5��28.5��E��28.5��30.5��ͳ�����������ɼ�ͳ�Ʊ�
| ������ | Ƶ��/�� | Ƶ�� |
| A | 12 | 0.05 |
| B | 36 | a |
| C | 84 | 0.35 |
| D | b | 0.25 |
| E | 48 | 0.20 |
��������ͨ������Ϣ���ش��������⣺
��1��ͳ�Ʊ��У�a=�� ����b=�� ��������ͳ��ͼ����������
��2��С��˵�����������ݵ�����һ����C�У�������ΪС����˵����ȷ���� �������ȷ��������
��3�����ɼ���27�����ϣ���27�֣���Ϊ���㣬����н���48000�������꼶ѧ���������ɼ�Ϊ�����ѧ������Լ�ж��٣�
ijС��20����ͥ������ˮ������λ���֣�ͳ�����£�
| ����ˮ������λ���֣� | 4 | 5 | 6 | 7 | 8 | 9 |
| ���� | 1 | 3 | 6 | 5 | 4 | 1 |
����20����ͥ����ˮ������������λ���ֱ��� ����ԭ����

 a3by�멁5a2yb4��ͬ�����������ͬ����ϲ��Ľ����
a3by�멁5a2yb4��ͬ�����������ͬ����ϲ��Ľ���� 
 ��(m2��1)�Ľ����(����)A����m2��2m��1 B����m2��2m��1 C��m2��2m��1 D��m2��1
��(m2��1)�Ľ����(����)A����m2��2m��1 B����m2��2m��1 C��m2��2m��1 D��m2��1 �н⣬��a��ֵΪ�� ��
�н⣬��a��ֵΪ�� �� C.a=1 D.������
C.a=1 D.������ B.
B.  C .
C .  D .
D . 