题目内容
已知A(1,0),B(0,1),问在x轴上是否存在点P,使得以P,A,B为顶点的三角形为等腰三角形.
考点:等腰三角形的判定,坐标与图形性质
专题:
分析:设点P的坐标为(x,0),分AB为腰和底及PA为底来进行讨论,再求得x即可.
解答:解:假设存在,设点P坐标为(x,0),则AP=|x-1|,
由A(1,0),B(0,1),可知OA=OB=1,AB=
,
当AB为底时,因为OA=OB,所以O点即为所求的P点,此时坐标为(0,0);
当AB为腰时,且AP为腰时,则有AB=AP=
,即|x-1|=
,解得x=
+1或1-
,此时P点坐标为(1+
,0)或(1-
,0);
当AB为腰时,且AP为底时,则有AO=OP=1,此时可知P点坐标为(-1,0);
综上可知存在点P,使得以P,A,B为顶点的三角形为等腰三角形,P点的坐标为(0,0)、(1+
,0)、(1-
,0)、(-1,0).
由A(1,0),B(0,1),可知OA=OB=1,AB=
| 2 |
当AB为底时,因为OA=OB,所以O点即为所求的P点,此时坐标为(0,0);
当AB为腰时,且AP为腰时,则有AB=AP=
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
当AB为腰时,且AP为底时,则有AO=OP=1,此时可知P点坐标为(-1,0);
综上可知存在点P,使得以P,A,B为顶点的三角形为等腰三角形,P点的坐标为(0,0)、(1+
| 2 |
| 2 |
点评:本题主要考查等腰三角形的判定,分情况讨论得出关于P点的横坐标x的方程是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
对当x=-1,y=-2时,代数式x2-2y+1的值是( )
| A、-1 | B、-2 | C、6 | D、4 |
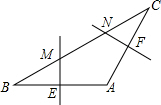 如图,在△ABC中,AB=AC,∠A=120°,BC=12cm,AB的垂直平分线交BC于点M,交AB于点E,AC的垂直平分线交BC于点N,交AC于点F,则MN的长为( )
如图,在△ABC中,AB=AC,∠A=120°,BC=12cm,AB的垂直平分线交BC于点M,交AB于点E,AC的垂直平分线交BC于点N,交AC于点F,则MN的长为( )