题目内容
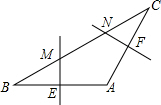 如图,在△ABC中,AB=AC,∠A=120°,BC=12cm,AB的垂直平分线交BC于点M,交AB于点E,AC的垂直平分线交BC于点N,交AC于点F,则MN的长为( )
如图,在△ABC中,AB=AC,∠A=120°,BC=12cm,AB的垂直平分线交BC于点M,交AB于点E,AC的垂直平分线交BC于点N,交AC于点F,则MN的长为( )| A、5cm | B、4cm |
| C、3cm | D、2cm |
考点:线段垂直平分线的性质
专题:
分析:首先连接AM,AN,由AB的垂直平分线交BC于点M,交AB于点E,AC的垂直平分线交BC于点N,交AC于点F,可得AM=BM,AN=CN,又由在△ABC中,AB=AC,∠A=120°,易证得△AMN是等边三角形,继而可得BM=MN=CN,即可求得答案.
解答: 解:连接AM,AN,
解:连接AM,AN,
∵AB的垂直平分线交BC于点M,交AB于点E,AC的垂直平分线交BC于点N,交AC于点F,
∴AM=BM,AN=CN,
∴∠BAM=∠B,∠CAN=∠C,
∵AB=AC,∠A=120°,
∴∠B=∠C=30°,
∴∠AMN=∠ANM=60°,
∴△AMN是等边三角形,
∴AM=MN=AN,
∴BM=MN=CN,
∵BC=12cm,
∴MN=4cm.
故选B.
 解:连接AM,AN,
解:连接AM,AN,∵AB的垂直平分线交BC于点M,交AB于点E,AC的垂直平分线交BC于点N,交AC于点F,
∴AM=BM,AN=CN,
∴∠BAM=∠B,∠CAN=∠C,
∵AB=AC,∠A=120°,
∴∠B=∠C=30°,
∴∠AMN=∠ANM=60°,
∴△AMN是等边三角形,
∴AM=MN=AN,
∴BM=MN=CN,
∵BC=12cm,
∴MN=4cm.
故选B.
点评:此题考查了线段垂直平分线的性质、等边三角形的判定与性质以及等腰三角形的性质.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下列计算中正确的是( )
| A、(-14)-(+5)=-9 |
| B、0-(-5)=5 |
| C、-3-3=0 |
| D、-5-2=-3 |
下列说法正确的是( )
| A、负数没有倒数 |
| B、正数的倒数比自身小 |
| C、任何有理数都有倒数 |
| D、倒数等于本身的数是-1或1 |
 如图,点A、B、C在⊙O上,OD⊥AB于点D,OE⊥CB于点E,弧AB度数为40°,弧CB的度数为50°,且DE=6,则⊙O半径的长度是
如图,点A、B、C在⊙O上,OD⊥AB于点D,OE⊥CB于点E,弧AB度数为40°,弧CB的度数为50°,且DE=6,则⊙O半径的长度是
 半径为2,AB为直径,C、D是
半径为2,AB为直径,C、D是