ЬтФПФкШн
ЁОЬтФПЁПРЯЪІИјЭЌбЇУЧВМжУСЫвЛИіЁАдкЦНУцФкеввЛЕуЃЌЪЙИУЕуЕНЕШбќШ§НЧаЮЕФШ§ИіЖЅЕуЕФОрРыЯрЕШЁБЕФГпЙцзїЭМШЮЮёЃК
ЯТУцЪЧаЁДЯЭЌбЇЩшМЦЕФГпЙцзїЭМЙ§ГЬЃК
вбжЊЃКШчЭМЃЌ![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ
ЧѓзїЃКвЛЕу![]() ЃЌЪЙЕУ
ЃЌЪЙЕУ![]() .
.
зїЗЈЃК
Ђйзї![]() ЕФЦНЗжЯп
ЕФЦНЗжЯп![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЛ
ЃЛ
ЂкзїБп![]() ЕФДЙжБЦНЗжЯп
ЕФДЙжБЦНЗжЯп![]() ЃЌ
ЃЌ![]() гы
гы![]() ЯрНЛгкЕу
ЯрНЛгкЕу![]() ЃЛ
ЃЛ
ЂлСЌНг![]() ЃЌ
ЃЌ
ЫљвдЃЌЕу![]() ОЭЪЧЫљЧѓзїЕФЕу.
ОЭЪЧЫљЧѓзїЕФЕу.
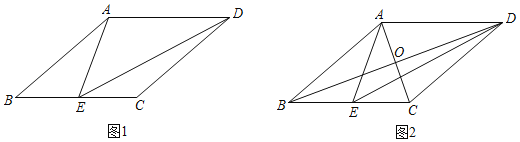
ИљОнаЁДЯЭЌбЇЩшМЦЕФГпЙцзїЭМЙ§ГЬЃЌ
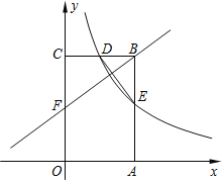
ЃЈ1ЃЉЪЙгУжБГпКЭдВЙцЃЌВЙШЋЭМаЮЃЈБЃСєзїЭМКлМЃЃЉ
ЃЈ2ЃЉЭъГЩЯТУцЕФжЄУї.
жЄУїЃКЁп![]() ЃЌ
ЃЌ![]() ЦНЗж
ЦНЗж![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЌ
ЃЌ
Ёр![]() ЪЧ
ЪЧ![]() ЕФДЙжБЦНЗжЯпЃЛЃЈ ЃЉЃЈЬюЭЦРэвРОнЃЉ
ЕФДЙжБЦНЗжЯпЃЛЃЈ ЃЉЃЈЬюЭЦРэвРОнЃЉ
Ёр![]() .
.
Ёп![]() ДЙжБЦНЗж
ДЙжБЦНЗж![]() ЃЌНЛ
ЃЌНЛ![]() гкЕу
гкЕу![]() ЃЌ
ЃЌ
Ёр![]() ЃЛЃЈ ЃЉЃЈЬюЭЦРэвРОнЃЉ
ЃЛЃЈ ЃЉЃЈЬюЭЦРэвРОнЃЉ
Ёр![]() .
.
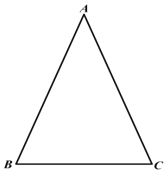
ЁОД№АИЁПЃЈ1ЃЉМћНтЮіЃЛЃЈ2ЃЉЕШбќШ§НЧаЮЕФШ§ЯпКЯвЛ ЯпЖЮДЙжБЦНЗжЯпЩЯЕФЕуЕНЯпЖЮСНЖЫЕуЕФОрРыЯрЕШ.
ЁОНтЮіЁП
ЃЈ1ЃЉРћгУЛљБОзїЭМзїНЧЦНЗжЯпADКЭABЕФДЙжБЦНЗжЯпЃЌЫќУЧЯрНЛгкPЕуЃЛ
ЃЈ2ЃЉИљОнЕШбќШ§НЧаЮЕФаджЪЕУЕНPB=PCЃЎдйИљОнЯпЖЮДЙжБЦНЗжЯпЩЯЕФЕуЕНЯпЖЮСНЖЫЕФОрРыЯрЕШЕУЕНPA=PCЃЌДгЖјЕУЕНPA=PB=PCЃЎ
ЃЈ1ЃЉШчЭМЃЌADЁЂЕуPЮЊЫљЧѓЃЛ

ЃЈ2ЃЉжЄУїЃКЁп![]() ЃЌ
ЃЌ![]() ЦНЗж
ЦНЗж![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЌ
ЃЌ
Ёр![]() ЪЧ
ЪЧ![]() ЕФДЙжБЦНЗжЯпЃЛЃЈ ЕШбќШ§НЧаЮЕФШ§ЯпКЯвЛ ЃЉЃЈЬюЭЦРэвРОнЃЉ
ЕФДЙжБЦНЗжЯпЃЛЃЈ ЕШбќШ§НЧаЮЕФШ§ЯпКЯвЛ ЃЉЃЈЬюЭЦРэвРОнЃЉ
Ёр![]() .
.
Ёп![]() ДЙжБЦНЗж
ДЙжБЦНЗж![]() ЃЌНЛ
ЃЌНЛ![]() гкЕу
гкЕу![]() ЃЌ
ЃЌ
Ёр![]() ЃЛЃЈ ЯпЖЮДЙжБЦНЗжЯпЩЯЕФЕуЕНЯпЖЮСНЖЫЕуЕФОрРыЯрЕШ ЃЉЃЈЬюЭЦРэвРОнЃЉ
ЃЛЃЈ ЯпЖЮДЙжБЦНЗжЯпЩЯЕФЕуЕНЯпЖЮСНЖЫЕуЕФОрРыЯрЕШ ЃЉЃЈЬюЭЦРэвРОнЃЉ
Ёр![]() .
.

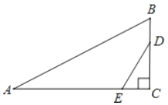
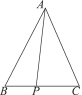
ЁОЬтФПЁПШчЭМЃЌЁЯMAN=30ЁуЃЌдкЩфЯпANЩЯШЁвЛЕуBЃЌЪЙAB=4 cmЃЌЙ§ЕуBзїBCЁЭAMгкЕуCЃЌЕуDЮЊБпABЩЯЕФЖЏЕуЃЈЕуDВЛгыЕуAЃЌЕуBжиКЯЃЉЃЌСЌНгCDЃЌЙ§ЕуDзїEDЁЭCDНЛжБЯпACгкЕуEЃЎдкЕуDгЩЕуAЕНЕуBдЫЖЏЙ§ГЬжаЃЌЩшAD=x cmЃЌAE=y cmЃЎ
ЃЈ1ЃЉШЁжИЖЈЕузїЭМЃЌИљОнЯТУцБэИёдЄЬюНсЙћЃЌЯШЭЈЙ§зїЭМШЗЖЈAD=2 cmЪБЃЌЕуEЕФЮЛжУЃЌВтСПAEЕФГЄЖШЃЎ
ЂйИљОнЬтвтЃЌдкД№ЬтПЈЩЯВЙШЋЭМаЮЃЛ
ЂкАбБэИёВЙГфЭъећЃКЭЈЙ§ШЁЕуЁЂЛЭМЁЂВтСПЃЌЕУЕНСЫxгыyЕФМИзщЖдгІжЕЃЌШчБэЃК
x/cm | Ё |
| 1 |
| 2 |
| 3 |
| Ё |
y cm | Ё | 0.4 | 0.8 | 1.0 | m | 1.0 | 0 | 4.0 | Ё |
дђm=______ЃЈНсЙћБЃСєвЛЮЛаЁЪ§ЃЉЃЎ
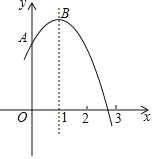
ЃЈ2ЃЉдкЯТУцЕФЦНУцжБНЧзјБъЯЕxOyжаЃЌУшГівдВЙШЋКѓЕФБэжаИїЖдЖдгІжЕЮЊзјБъЕФЕуЃЌЛГіИУКЏЪ§ЕФЭМЯѓЃЛ
ЃЈ3ЃЉНсКЯЛГіЕФКЏЪ§ЭМЯѓЃЌНтОіЮЪЬтЃКЕБAE=![]() ADЪБЃЌADЕФГЄЖШдМЮЊ______cmЃЎ
ADЪБЃЌADЕФГЄЖШдМЮЊ______cmЃЎ