Question

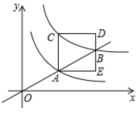
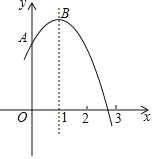
【题目】如图，抛物线y＝﹣x2+2x+2交y轴于点A，与x轴的一个交点在2和3之间，顶点为B．下列说法：其中正确判断的序号是（　　）

①抛物线与直线y＝3有且只有一个交点；

②若点M（﹣2,y1），N（1,y2），P（2,y3）在该函数图象上，则y1＜y2＜y3；

③将该抛物线先向左，再向下均平移2个单位，所得抛物线解析式为y＝（x+1）2+1；

④在x轴上找一点D，使AD+BD的和最小，则最小值为．

A.①②④B.①②③C.①③④D.②③④

Answer 1

【答案】C

【解析】

根据抛物线的性质和平移，以及一动点到两定点距离之和最小问题的处理方法，对选项进行逐一分析即可.

①抛物线的顶点，则抛物线与直线y＝3有且只有一个交点，正确，符合题意；

②抛物线x轴的一个交点在2和3之间，

则抛物线与x轴的另外一个交点坐标在x＝0或x＝﹣1之间，

则点N是抛物线的顶点为最大，点P在x轴上方，点M在x轴的下放，

故y1＜y3＜y2，故错误，不符合题意；

③y＝﹣x2+2x+2＝﹣（x+1）2+3，将该抛物线先向左，再向下均平移2个单位，

所得抛物线解析式为y＝（x+1）2+1，正确，符合题意；

④点A关于x轴的对称点，连接A′B交x轴于点D，

则点D为所求，距离最小值为BD′＝＝，

正确，符合题意；

故选：C．