题目内容
12.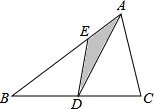 已知S△ABC=1,D是BC的中点,AE:EB=1:2,求△ADE的面积.
已知S△ABC=1,D是BC的中点,AE:EB=1:2,求△ADE的面积.
分析 首先根据AE:EB=1:2,可得△BDE的面积是△ADE的面积的2倍,然后根据三角形的中线将三角形分成面积相等的两部分,用△ABC的面积除以2,求出△ABD的面积是多少,进一步得到△ADE的面积是多少.
解答 解:∵AE:EB=1:2,
∴△BDE的面积是△ADE的面积的2倍,
∵S△ABC=1,D是BC的中点,
∴△ABD的面积是$\frac{1}{2}$,
∴△ADE的面积是:$\frac{1}{2}$×$\frac{1}{2+1}$=$\frac{1}{6}$.
故△ADE的面积是$\frac{1}{6}$.
点评 此题主要考查了三角形的面积的求法,以及三角形的中线的特征,要熟练掌握,解答此题的关键是要明确:(1)三角形的中线将三角形分成面积相等的两部分;(2)两个三角形的高相同时,面积的比等于它们的底边的比.

练习册系列答案
相关题目
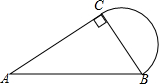 如图,在Rt△ABC中,AC=5cm,AB=7cm,以BC为直径画半圆,求半圆的面积.
如图,在Rt△ABC中,AC=5cm,AB=7cm,以BC为直径画半圆,求半圆的面积.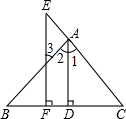 如图,AD⊥BC,垂足为点D,EF⊥BC,垂足为点F,且AD平分∠BAC,试说明∠3=∠E.
如图,AD⊥BC,垂足为点D,EF⊥BC,垂足为点F,且AD平分∠BAC,试说明∠3=∠E.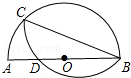 以半圆中的一条弦BC(非直径)为对称轴将弧BC折叠后与直径AB交于点D,若$\frac{AD}{DB}$=$\frac{2}{3}$,且AB=10,则CB的长为4$\sqrt{5}$.
以半圆中的一条弦BC(非直径)为对称轴将弧BC折叠后与直径AB交于点D,若$\frac{AD}{DB}$=$\frac{2}{3}$,且AB=10,则CB的长为4$\sqrt{5}$.