题目内容
在平原上,一门迫击炮发射的一发炮弹飞行的高度y(m)与飞行时间x(s)的关系满足:y=-
x2+10x.
(1)经过一定时间,炮弹能否达到126m的高度?为什么?
(2)经过多长时间,炮弹落到地上爆炸?
| 1 | 5 |
(1)经过一定时间,炮弹能否达到126m的高度?为什么?
(2)经过多长时间,炮弹落到地上爆炸?
分析:(1)把一般化成顶点式,顶点坐标的横坐标即达到最高点的时间;
(2)炮弹落到地上,即关系式的y值为零,再求出适合的x的值即可.
(2)炮弹落到地上,即关系式的y值为零,再求出适合的x的值即可.
解答:解:(1)把一般式化成顶点式y=-
x2+10x=-
(x-25)2+125,
当x=25时,y=-
(25-25)2+125=125,
即经过25秒,炮弹到达它的最高点,最高点的高度是125m,故不能达到126m的高度;
(2)由题意得:-
x2+10x=0
解得:x1=50,x2=0(不合题意,舍去)
即经过50s,炮弹落到地上爆炸.
| 1 |
| 5 |
| 1 |
| 5 |
当x=25时,y=-
| 1 |
| 5 |
即经过25秒,炮弹到达它的最高点,最高点的高度是125m,故不能达到126m的高度;
(2)由题意得:-
| 1 |
| 5 |
解得:x1=50,x2=0(不合题意,舍去)
即经过50s,炮弹落到地上爆炸.
点评:本题主要考查了二次函数的顶点坐标及求解方法,正确根据二次函数最值以及图象与坐标轴交点分析得出是解题关键.

练习册系列答案
相关题目
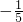 x2+10x.
x2+10x. .
. .
.