Question

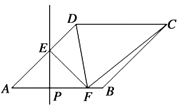
【题目】如图，在菱形ABCD中，∠DAB=45°，AB=4，点P为线段AB上一动点（不与点A重合），过点P作PE⊥AB交射线AD于点E，沿PE将△APE折叠，点A的对称点为点F，连接EF，DF，CF，当△CDF为等腰三角形时，AP的长为________．

Answer 1

【答案】2，或

【解析】

根据题意分DF=CD、CF=CD或FD=FC三种情况先得出相应的图形，由此进一步结合相关信息加以分析即可.

如图1，当DF=CD时，点F在点处，作DN⊥AB于点N，

∵四边形ABCD是菱形，AB=4，

∴CD=AD=4，

在Rt△AND中，

∵∠DAN=45°，AD=4，

∴DN=AN=，

又∵DA=D，且DN⊥AB，

∴N=AN=，

∴AP=；

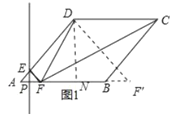
如图2，当CF=CD=4时，点F与点B重合或在点处，

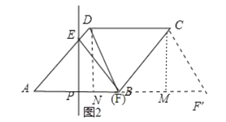
①点F与点B重合时，则PE是AB的垂直平分线，

∴AP=；

②点F在点处时，过点C作CM⊥AB于点M，

易得：∠DAB=∠=45°，CB==4，

∴CM==BM=，

∴=，

∴AP=，

此时点E不在线段AD上，舍去；

如图3，当FD=FC时，过点F作FQ⊥CD于点Q，交BC于点G，

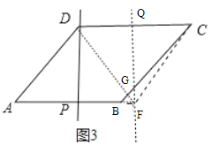
则：CQ=DQ=QG=2，FQ=，

∴BF=GF=，

∴AF=，

∴AP=；

综上所述，AP的长度为：2，或，

故答案为：2，或.