题目内容
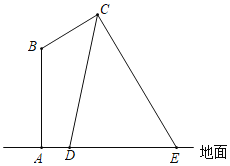
【题目】如图,![]() 是垂直于水平面的建筑物,为测量
是垂直于水平面的建筑物,为测量![]() 的高度,小红从建筑物底端
的高度,小红从建筑物底端![]() 出发,沿水平方向行走了52米到达点
出发,沿水平方向行走了52米到达点![]() ,然后沿斜坡
,然后沿斜坡![]() 前进,到达坡顶
前进,到达坡顶![]() 点处,
点处,![]() .在点
.在点![]() 处放置测角仪,测角仪支架
处放置测角仪,测角仪支架![]() 高度为0.8米,在
高度为0.8米,在![]() 点处测得建筑物顶端
点处测得建筑物顶端![]() 点的仰角
点的仰角![]() 为
为![]() (点
(点![]() ,
,![]() ,
,![]() ,
,![]() 在同一平面内),斜坡
在同一平面内),斜坡![]() 的坡度(或坡比)
的坡度(或坡比)![]() ,求建筑物
,求建筑物![]() 的高度.(精确到个位)(参考数据:
的高度.(精确到个位)(参考数据:![]() )
)
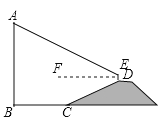
【答案】建筑物![]() 的高度约为72米
的高度约为72米
【解析】
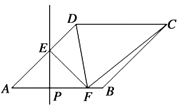
过点E作EM⊥AB,垂足为M,设DG=x,则CG=2.4x,利用勾股定理求出x的值,进而可得出CG的长,故可得出EG的长.由矩形的判定定理得出四边形EGBM是矩形,故可得出EM=BG,BM=EG,再由锐角三角函数的定义求出AM的长,进一步即可求得AB.
解:过点E作EM⊥AB,垂足为M,延长ED交BC于G,

∵斜坡![]() 的坡度(或坡比)
的坡度(或坡比)![]() ,
,![]() 米,
米,
∴设![]() 米,则
米,则![]() 米,
米,
在![]() 中,
中,![]() ,
,
![]() 解得
解得![]()
∴DG=20米,![]() 米,
米,
∴![]() 米,
米,![]() 米
米
∵![]() ,
,![]() ,
,![]()
∴四边形![]() 是矩形.
是矩形.
∴![]() 米,
米,![]() 米.
米.
在![]() 中,
中,
∵![]()
∴![]() 米
米
∴![]() (米).
(米).
答:建筑物![]() 的高度约为72米.
的高度约为72米.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
【题目】如图,正方形ABCD内部有若干个点,则用这些点以及正方形ABCD的顶点A、B、C、D把原正方形分割成一些三角形(互相不重叠):
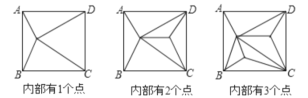
(1)填写下表:
正方形ABCD内点的个数 | 1 | 2 | 3 | 4 | ... | n |
分割成三角形的个数 | 4 | 6 | _____ | _____ | ... | _____ |
(2)原正方形能否被分割成2021个三角形?若能,求此时正方形ABCD内部有多少个点?若不能,请说明理由.