题目内容
16.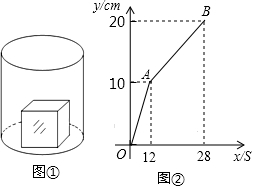 如图①,一个正方体铁块放置在圆柱形水槽内,现以一定的速度往水槽中注水,28s时注满水槽.水槽内水面的高度y(cm)与注水时间x(s)之间的函数图象如图②所示.
如图①,一个正方体铁块放置在圆柱形水槽内,现以一定的速度往水槽中注水,28s时注满水槽.水槽内水面的高度y(cm)与注水时间x(s)之间的函数图象如图②所示.(1)正方体的棱长为10cm;
(2)求线段AB对应的函数解析式,并写出自变量x的取值范围;
(3)如果将正方体铁块取出,又经过t(s)恰好将此水槽注满,直接写出t的值.
分析 (1)直接利用一次函数图象结合水面高度的变化得出正方体的棱长;
(2)直接利用待定系数法求出一次函数解析式,再利用函数图象得出自变量x的取值范围;
(3)利用一次函数图象结合水面高度的变化得出t的值.
解答 解:(1)由题意可得:12秒时,水槽内水面的高度为10cm,12秒后水槽内高度变化趋势改变,
故正方体的棱长为10cm;
故答案为:10;
(2)设线段AB对应的函数解析式为:y=kx+b,
∵图象过A(12,10),B(28,20),
∴$\left\{\begin{array}{l}{12k+b=10}\\{28k+b=20}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=\frac{5}{8}}\\{b=\frac{5}{2}}\end{array}\right.$,
∴线段AB对应的解析式为:y=$\frac{5}{8}$x+$\frac{5}{2}$(12≤x≤28);
(3)∵28-12=16(s),
∴没有立方体时,水面上升10cm,所用时间为:16秒,
∵前12秒由立方体的存在,导致水面上升速度加快了4秒,
∴将正方体铁块取出,经过4秒恰好将此水槽注满.
点评 此题主要考查了一次函数的应用,正确利用函数图象获取正确信息是解题关键.

练习册系列答案
相关题目
3.二次函数y=ax2+bx+c(a,b,c为常数且a≠0)中的x与y的部分对应值如表:
已知表中有且只有一组数据错误,则这组错误数据中的x值是2.
| x | … | -1 | 0 | 1 | 2 | 3 | … |
| y | … | 0 | -3 | -4 | 1 | 0 | … |
 如图,分别以正五边形ABCDE的顶点A,D为圆心,以AB长为半径画$\widehat{BE}$,$\widehat{CE}$.若AB=1,则阴影部分图形的周长为$\frac{6}{5}$π+1(结果保留π).
如图,分别以正五边形ABCDE的顶点A,D为圆心,以AB长为半径画$\widehat{BE}$,$\widehat{CE}$.若AB=1,则阴影部分图形的周长为$\frac{6}{5}$π+1(结果保留π).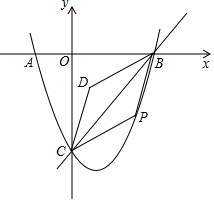 如图,在平面直角坐标系中,抛物线y=x2+bx+c与x轴交于点A(-1,0),B(3,0),与y轴交于点C,作直线BC,点P是抛物线上一个动点(点P不与点B,C重合),连结PB,PC,以PB,PC为边作?CPBD,设?CPBD的面积为S,点P的横坐标为m.
如图,在平面直角坐标系中,抛物线y=x2+bx+c与x轴交于点A(-1,0),B(3,0),与y轴交于点C,作直线BC,点P是抛物线上一个动点(点P不与点B,C重合),连结PB,PC,以PB,PC为边作?CPBD,设?CPBD的面积为S,点P的横坐标为m.